题目内容
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为______.
的图象经过点B,则k的值为______.
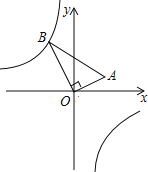
【答案】﹣8.
【解析】根据∠AOB=90°,先过点A作AC⊥x轴,过点B作BD⊥x轴,构造相似三角形,再利用相似三角形的对应边成比例,列出比例式进行计算,求得点B的坐标,进而得出k的值.
解:过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,
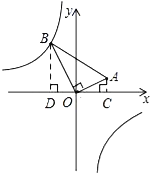
则∠OCA=∠BDO=90°,∴∠DBO+∠BOD=90°,
∵∠AOB=90°,∴∠AOC+∠BOD=90°,∴∠DBO=∠AOC,
∴△DBO∽△COA,∴![]() ,
,
∵点A的坐标为(2,1),∴AC=1,OC=2,∴AO=![]() =
=![]() ,
,
∴![]() ,即BD=4,DO=2,∴B(﹣2,4),
,即BD=4,DO=2,∴B(﹣2,4),
∵反比例函数y=![]() 的图象经过点B,∴k的值为﹣2×4=﹣8.
的图象经过点B,∴k的值为﹣2×4=﹣8.
故答案为:﹣8.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目