题目内容
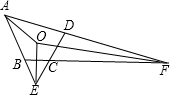
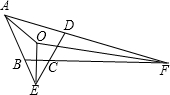 如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=________.
如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=________.
95°
分析:根据三角形的外角性质求出∠EOF=∠EAF+ ∠AFB+
∠AFB+ ∠AED,∠BCD=∠AFB+∠CDF,代入求出∠EOF=
∠AED,∠BCD=∠AFB+∠CDF,代入求出∠EOF= (∠EAF+∠BCD),代入求出即可.
(∠EAF+∠BCD),代入求出即可.
解答:∵角AED,角AFB平分线交于O,
∴∠EOF=∠OAB+ ∠AFB+∠OAD+
∠AFB+∠OAD+ ∠AED,
∠AED,
=∠EAF+ ∠AFB+
∠AFB+ ∠AED ①,
∠AED ①,
又∠BCD=∠AFB+∠CDF,
=∠AFB+∠EAF+∠AED ②,
由①②得∠EOF=∠EAF+ ∠AFB+
∠AFB+ ∠AED
∠AED
= (∠EAF+∠EAF+∠AFB+∠AED)
(∠EAF+∠EAF+∠AFB+∠AED)
= ∠EAF+
∠EAF+ ∠BCD
∠BCD
= ×60°+
×60°+ ×130°
×130°
=95°.
故答案为:95°.
点评:本题主要考查对三角形的内角和定理,三角形的外角性质等知识点的理解和掌握,能熟练地运用性质进行推理和计算是解此题的关键.
分析:根据三角形的外角性质求出∠EOF=∠EAF+
 ∠AFB+
∠AFB+ ∠AED,∠BCD=∠AFB+∠CDF,代入求出∠EOF=
∠AED,∠BCD=∠AFB+∠CDF,代入求出∠EOF= (∠EAF+∠BCD),代入求出即可.
(∠EAF+∠BCD),代入求出即可.解答:∵角AED,角AFB平分线交于O,
∴∠EOF=∠OAB+
 ∠AFB+∠OAD+
∠AFB+∠OAD+ ∠AED,
∠AED,=∠EAF+
 ∠AFB+
∠AFB+ ∠AED ①,
∠AED ①,又∠BCD=∠AFB+∠CDF,
=∠AFB+∠EAF+∠AED ②,
由①②得∠EOF=∠EAF+
 ∠AFB+
∠AFB+ ∠AED
∠AED=
 (∠EAF+∠EAF+∠AFB+∠AED)
(∠EAF+∠EAF+∠AFB+∠AED)=
 ∠EAF+
∠EAF+ ∠BCD
∠BCD=
 ×60°+
×60°+ ×130°
×130°=95°.
故答案为:95°.
点评:本题主要考查对三角形的内角和定理,三角形的外角性质等知识点的理解和掌握,能熟练地运用性质进行推理和计算是解此题的关键.

练习册系列答案
相关题目
 11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为
11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为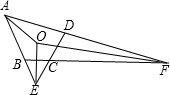 如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=
如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=