无论m为何实数.直线y=-x+2m与y=x+4的交点不可能在( )A．第一象限B．第二象限C．第三象限D．第四象限题目和参考答案——青夏教育精英家教网——

题目内容

11．无论m为何实数，直线y=-x+2m与y=x+4的交点不可能在（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

分析根据一次函数的图象与系数的关系即可得出结论．

解答解：∵一次函数y=x+4中，k=1＞0，b=4＞0，
∴函数图象经过一二三象限，
∴无论m为何实数，直线y=-x+2m与y=x+4的交点不可能在第四象限．
故选D．

点评本题考查的是两条直线相交或平行问题，熟知一次函数的图象与系数的关系是解答此题的关键．

练习册系列答案

高中练习册系列答案

金钥匙阅读书系系列答案

中考必备考点分类卷系列答案

新思维冲刺小升初达标总复习系列答案

课时练优选卷系列答案

金榜小状元系列答案

单元自测题同步达标测试卷系列答案

小考练兵场系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

相关题目

2．$\frac{1}{2}$x-2（x-$\frac{1}{3}$y²）+（-$\frac{2}{3}$x+$\frac{1}{3}$y²），其中x=-2，y=-$\frac{2}{3}$．

2．材料：一般地，n个相同因数a相乘：$\underset{\underbrace{a•a•a…a•a}}{n个a}$记为aⁿ．如2³=8，此时，3叫做以2为底的8的对数，记为log₂8（即log₂8=3）．那么，log₃9=2，（log₂16）²+$\frac{1}{3}$log₃81=17$\frac{1}{3}$．

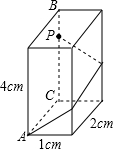如图，长方体的底面边长分别为1cm 和2cm，高为4cm，点P在边BC上，BP=$\frac{1}{4}$BC．若一只蚂蚁从A点开始经过3个侧面爬行一圈到达P点，则蚂蚁爬行的最短路径长为5cm．

6．下列计算正确的是（　　）

2$\sqrt{2}$+4$\sqrt{3}$=6$\sqrt{5}$

3$\sqrt{2}$-2$\sqrt{2}$=1

$\sqrt{24}$÷$\sqrt{6}$=4

$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$

16．在半径为4cm的圆中，弧长为πcm的弧所对的圆周角的度数是22.5°．

3．（1）x²+kx+9是完全平方式，则k=±6．
（2）分解因式：9x³-18x²+9x=9x（x-1）²．

20．近似数0.020精确到千分位，它有2个有效数字．
近似数5.2万精确到千位，它有2个有效数字．

18．化简$\frac{\sqrt{-{a}^{3}}}{-a}$的结果是（　　）