Question

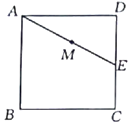
【题目】如图，正方形的边长为，点为边上一点，，点为的中点，过点作直线分别与，相交于点，.若，则长为______.

Answer 1

【答案】1或2

【解析】

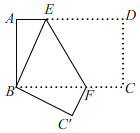
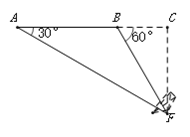
根据题意画出图形，过P作PN⊥BC，交BC于点N，由ABCD为正方形，得到AD=DC=PN，在直角三角形ADE中，利用锐角三角函数定义求出DE的长，进而利用勾股定理求出AE的长，根据M为AE中点求出AM的长，利用HL得到三角形ADE与三角形PQN全等，利用全等三角形对应边，对应角相等得到DE=NQ，∠DAE=∠NPQ=30°，再由PN与DC平行，得到∠PFA=∠DEA=60°，进而得到PM垂直于AE，在直角三角形APM中，根据AM的长，利用锐角三角函数定义求出AP的长，再利用对称性确定出AP′的长即可．

根据题意画出图形，过点作，交于点，交于点，四边形为正方形，.

在中，，cm，

cm.

根据勾股定理得cm.

为的中点，cm，

在和中，

，

，.

，，

，即.

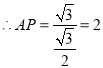在中，， cm.

由对称性得到 cm，

综上，等于1cm或2cm.

故答案为：1或2.