题目内容
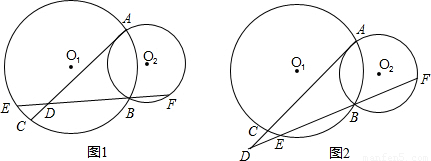
(2003•淮安)已知:⊙O1与⊙O2相交于点A、B,AC切⊙O2于点A,交⊙O1于点C.直线EF过点B,交⊙O1于点E,交⊙O2于点F.(1)设直线EF交线段AC于点D(如图1).
①若ED=12,DB=25,BF=11,求DA和DC的长;
②求证:AD•DE=CD•DF;
(2)当直线EF绕点B旋转交线段AC的延长线于点D时(如图2),试问AD•DE=CD•DF是否仍然成立?证明你的结论.
【答案】分析:(1)①有ED,BD,BF的长,根据切割线定理,可求出AD的长,然后根据相交弦定理可求出CD的长;②根据切割线定理得出的AD2=DB•BF以及相交弦定理得出的AD•CD=DE•BD,两式子相除即可得出所求的结论.
(2)解法与(1)中的②完全相同.
解答:解:(1)①∵AC切⊙O2于A,
∴AD2=DB•DF=25×36.
∴AD=30.
又由AD•CD=DE•BD得CD=10,
∴AD=30,CD=10.
②由AD2=DB•DF和AD•CD=DE•BD,
相除可得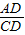 =
=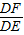 ,故AD•DE=CD•DF.
,故AD•DE=CD•DF.
(2)成立,
证明:∵AD切⊙O2于A,
∴AD2=DB•DF…①
又由DA•CD=DE•DB …②
①÷②得: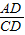 =
=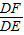 ,因此AD•DE=CD•DF.
,因此AD•DE=CD•DF.
点评:本题主要考查了相似三角形的判定和性质的应用以及切割线定理和相交弦定理.
(2)解法与(1)中的②完全相同.
解答:解:(1)①∵AC切⊙O2于A,
∴AD2=DB•DF=25×36.
∴AD=30.
又由AD•CD=DE•BD得CD=10,
∴AD=30,CD=10.
②由AD2=DB•DF和AD•CD=DE•BD,
相除可得
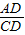 =
=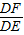 ,故AD•DE=CD•DF.
,故AD•DE=CD•DF.(2)成立,
证明:∵AD切⊙O2于A,
∴AD2=DB•DF…①
又由DA•CD=DE•DB …②
①÷②得:
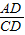 =
=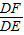 ,因此AD•DE=CD•DF.
,因此AD•DE=CD•DF.点评:本题主要考查了相似三角形的判定和性质的应用以及切割线定理和相交弦定理.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
(2003•淮安)已知二次函数y=ax2-4x+3的图象经过点(-1,8).
(1)求此二次函数的解析式;
(2)根据(1)填写下表.在直角坐标系中描点,并画出函数的图象;
(3)根据图象回答:当函数值y<0时,x的取值范围是什么?
(1)求此二次函数的解析式;
(2)根据(1)填写下表.在直角坐标系中描点,并画出函数的图象;
| x | 1 | 2 | 3 | 4 | |
| y |
(2003•淮安)已知二次函数y=ax2-4x+3的图象经过点(-1,8).
(1)求此二次函数的解析式;
(2)根据(1)填写下表.在直角坐标系中描点,并画出函数的图象;
(3)根据图象回答:当函数值y<0时,x的取值范围是什么?
(1)求此二次函数的解析式;
(2)根据(1)填写下表.在直角坐标系中描点,并画出函数的图象;
| x | 1 | 2 | 3 | 4 | |
| y |

