题目内容
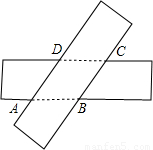
将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD。
(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么菱形ABCD的周长是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由。
(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么菱形ABCD的周长是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由。

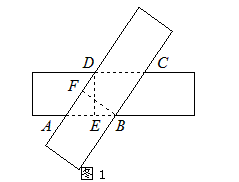
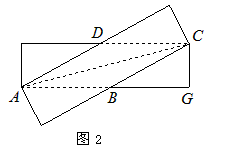
| 解:(1)如图1,因为AD∥BC,AB∥DC, 所以四边形ABCD为平行四边形, 分别过点B、D作BF⊥AD,DE⊥AB,垂足分别为点E、F, 则BE=CF, 因为∠DAB=∠BAF, 所以Rt△DAB≌Rt△BAF, 所以AD=AB, 所以四边形ABCD为菱形; (2)存在最小值和最大值, ①当∠DAB=90°时,菱形ABCD为正方形,周长最小值为8; ②当AC为矩形纸片的对角线时,设AB=x,如图2, 在Rt△BCG中, 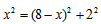 , ,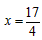 , ,所以周长最大值为17。 |
  |

练习册系列答案
相关题目
 11、将两张宽度相等的矩形叠放在一起得到如图所示的四边形ABCD,则四边形ABCD是
11、将两张宽度相等的矩形叠放在一起得到如图所示的四边形ABCD,则四边形ABCD是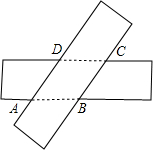 将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.
将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.