题目内容
【题目】折纸是一项有趣的活动,在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念. 今天,就让我们带着数学的眼光来玩一玩折纸.
实践操作
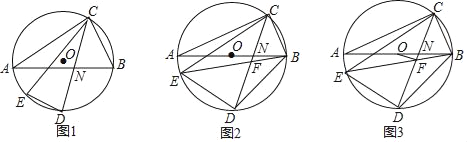
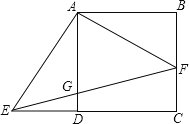
如图1,将矩形纸片ABCD沿对角线AC翻折,使点![]() 落在矩形ABCD所在平面内,
落在矩形ABCD所在平面内,![]() C和AD相交于点E,连接
C和AD相交于点E,连接![]() D.
D.
解决问题
(1)在图1中,①![]() D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
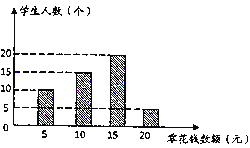
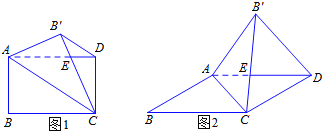
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
拓展应用
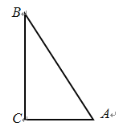
(3)在图2中,若∠B=30o,AB=![]() ,当A
,当A![]() ⊥AD时,BC的长度为_____.
⊥AD时,BC的长度为_____.
【答案】(1) BD′∥AC,菱形;(2)成立,理由见解析;(3)4或6或8或12.
【解析】
(1)①根据内错角相等两直线平行即可判断;
②根据菱形的判定方法即可解决问题;
(2)只要证明AE=EC,即可证明结论②成立;只要证明∠ADB′=∠DAC,即可推出B′D∥AC;
(3)先证得四边形ACB′D是等腰梯形,分四种情形分别讨论求解即可解决问题;
解:(1)①BD′∥AC.②将△AEC剪下后展开,得到的图形是菱形;
故答案为BD′∥AC,菱形;
(2)①选择②证明如下:
如图2,
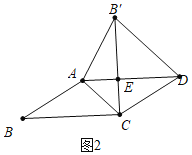
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵将△ABC沿AC翻折至△AB′C,
∴∠ACB′=∠ACB,
∴∠DAC=∠ACB′,
∴AE=CE,
∴△AEC是等腰三角形;
∴将△AEC剪下后展开,得到的图形四边相等,
∴将△AEC剪下后展开,得到的图形四边是菱形.
②选择①证明如下,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵将△ABC沿AC翻折至△AB′C,
∵B′C=BC,
∴B′C=AD,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD
∴∠ADB′=∠DAC,
∴B′D∥AC.
(3)∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠B=30°,∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
当∠B′AD=90°,AB>BC时,如图3中,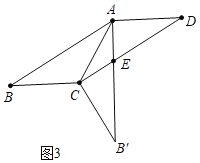
设∠ADB′=∠CB′D=y,
∴∠AB′D=y-30°,
解得y=60°,
∴∠AB′D=y-30°=30°,
∵AB′=AB=4![]()
![]()
∴BC=4,
当∠ADB′=90°,AB>BC时,如图4,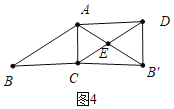
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=4![]()
![]()
当∠B′AD=90°,AB<BC时,如图5,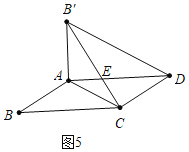
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
![]()
∴∠AB′C=30°,
∴AE=4,BE′=2AE=8,
∴AE=EC=4,
∴CB′=12,
当∠AB′D=90°时,如图6,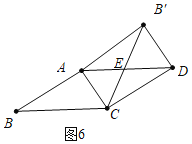
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是平行四边形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
![]()
![]()
∴已知当BC的长为4或6或8或12时,△AB′D是直角三角形.
故答案为:4或6或8或12;

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案