题目内容
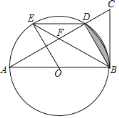
【题目】如图，以
的边
为直径画
，交
于点
，半径
，连接
，
，
，设交于点
，若
．
（1）求证：
是的切线；
（2）若
，求图中阴影部分的面积．
【答案】（1）证明见解析；（2）
.
【解析】
（1）求出∠ADB的度数，求出∠ABD+∠DBC=90°，根据切线的判定定理即可得出结论；
（2）连接OD，分别求出三角形DOB面积和扇形DOB面积，即可求出答案．
（1）∵AB是⊙O的直径，∴∠ADB=90°，∴∠A+∠ABD=90°．
∵∠A=∠DEB，∠DEB=∠DBC，∴∠A=∠DBC．
∴∠DBC+∠ABD=90°，∴BC是⊙O的切线；
（2）连接OD．
∵BF=BC=2，且∠ADB=90°，∴∠CBD=∠FBD．
∵OE∥BD，∴∠FBD=∠OEB．
∵OE=OB，∴∠OEB=∠OBE，∴∠CBD=∠OEB=∠OBE=
∠ABC=
90°=30°，∴∠C=60°，∴AB=
BC=2，∴⊙O的半径为，∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=
．
练习册系列答案
阅读快车系列答案
相关题目
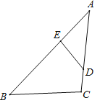
【题目】某中学举行“中国梦·校园好声音”歌手大赛，高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩（满分100）如下图所示：
根据图示信息，整理分析数据如下表：
平均数（分） | 中位数（分） | 众数（分） | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
（说明：图中虚线部分的间隔距离均相等）
（1）求出表格中
的值；
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．
