题目内容
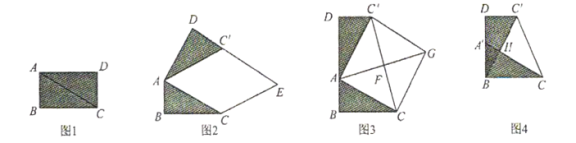
【题目】已知四边形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,
边上的点,![]() 与
与![]() 交于点
交于点![]() .
.
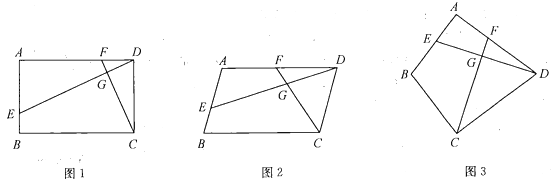
(1)如图1,若四边形![]() 是矩形,且
是矩形,且![]() ,求证:
,求证:![]() ;
;
(2)如图2,若四边形![]() 是平行四边形,试探究:当
是平行四边形,试探究:当![]() 与
与![]() 满足什么关系时,使得
满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图3,若![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)当![]() 时,
时,![]() 成立.(3)
成立.(3)![]()
【解析】
(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)当∠B+∠EGC=180°时,![]() 成立,证△DFG∽△DEA,得出
成立,证△DFG∽△DEA,得出![]() ,证△CGD∽△CDF,得出
,证△CGD∽△CDF,得出![]() ,即可得出答案;
,即可得出答案;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=![]() x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程
x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程![]() ,求出
,求出![]() ,证出△AED∽△NFC,即可得出答案.
,证出△AED∽△NFC,即可得出答案.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴![]()
(2)当∠B+∠EGC=180°时,![]() 成立.
成立.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EGC=180°,
∴∠A=∠EGC=∠FGD,
∵∠FDG=∠EDA,
∴△DFG∽△DEA,
∴![]()
∵∠B=∠ADC,∠B+∠EGC=180°,∠EGC+∠DGC=180°,
∴∠CGD=∠CDF,
∵∠GCD=∠DCF,
∴△CGD∽△CDF,
![]()
![]()
![]()
即当∠B+∠EGC=180°时,![]() 成立.
成立.
(3)解:![]()
理由是:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
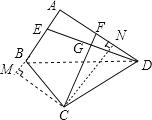
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
![]()
![]()
![]()
在Rt△CMB中,![]() ,BM=AM-AB=x-6,
,BM=AM-AB=x-6,
由勾股定理得:BM2+CM2=BC2,
![]()
x=0(舍去),![]()
![]()
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?