题目内容
好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.

(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.

(1)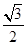 ;(2)
;(2)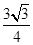 .(3)这三边能构成直角三角形.
.(3)这三边能构成直角三角形.
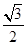 ;(2)
;(2)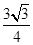 .(3)这三边能构成直角三角形.
.(3)这三边能构成直角三角形.试题分析:(1)分别过A2、C1作x轴的垂线,垂足分别为E、F,根据勾股定理求得相应线段的长度,由△A2C1B1=S梯形A1EFC1-△C1FB1-△A2EB1可求得;
(2)分别计算△A4B3B4、△A4OB4的面积,利用相似三角形即可求出△A4C3B3的面积;
(3)根据勾股定理的逆定理即可判定三角形为直角三角形.
试题解析:(1)
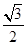 ;
;(2)解得△A4B3B4的面积为:
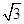
解得△A4OB4的面积为:
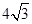
利用△OC3B3∽△OA4B4得:S四边形C3B3B4A4:S△OA4B4=7:16
∴四边形C3B3B4A4的面积为:
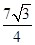
∴△A4C3B3的面积为:
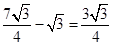 .
.(3)能.
设这些等腰三角形的高为h.
则:OA22=9+h2,
OA32=25+h2,
OA42=64
∵OA4=OB4
∴∠OA4B=∠OB4A4=∠A4B3B4
∴△OA4B4∽△A4B4B3
∴

∴A4B4=4
∴h2=15
∴OA22+OA32=OA42
即这三边能构成直角三角形.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
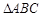 ∽
∽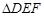 且对应高之比为2:3,那么
且对应高之比为2:3,那么
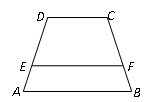
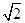 ,点A的坐标为(1,0),则E点的坐标为( )
,点A的坐标为(1,0),则E点的坐标为( )

 ,则
,则 的值是( )
的值是( )
