题目内容
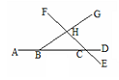
如图所示,已知AB∥CD,EF交AB于M交CD于F,MN⊥EF于M,MN交CD于N,若∠BME=110°,则∠MND=_____.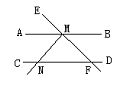

20°
根据对顶角相等求出∠AMF,再求出∠AMN,然后根据两直线平行,内错角相等求解即可.
解:∵∠BME=110°,
∴∠AMF=∠BME=110°,
∵MN⊥EF于M,
∴∠NMF=90°,
∴∠AMN=∠AMF-∠NMF=110°-90°=20°,
∵AB∥CD,
∴∠MND=∠AMN=20°.
故答案为:20°.
本题考查了平行线的性质,对顶角相等的性质,以及垂直的定义,是基础题,熟记性质并准确识图是解题的关键.
解:∵∠BME=110°,
∴∠AMF=∠BME=110°,
∵MN⊥EF于M,
∴∠NMF=90°,
∴∠AMN=∠AMF-∠NMF=110°-90°=20°,
∵AB∥CD,
∴∠MND=∠AMN=20°.
故答案为:20°.
本题考查了平行线的性质,对顶角相等的性质,以及垂直的定义,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
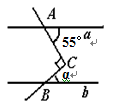
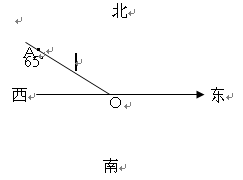
 方向
方向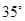 方向
方向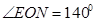 ,求
,求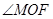 的度数;
的度数;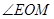 与
与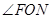 的大小,并写出理由;⑶求
的大小,并写出理由;⑶求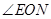 +
+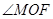 的度数.
的度数.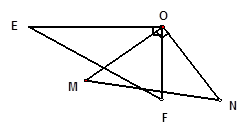
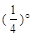 =__ __
=__ __ ′
′