题目内容
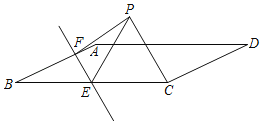
【题目】如图,在平行四边形ABCD中,AB=4,BC=4![]() ,∠D=30°,点E是BC边的中点,F是射线BA上一动点,将△BEF沿直线EF折叠,得到△PEF,连接PC,当△PCE为等边三角形时,BF的长为_____.
,∠D=30°,点E是BC边的中点,F是射线BA上一动点,将△BEF沿直线EF折叠,得到△PEF,连接PC,当△PCE为等边三角形时,BF的长为_____.
【答案】3或6
【解析】
分两种情况:当P点在EC的上方和下方时,由等边三角形的性质与直角三角形的性质分别求出BF的值即可.
当点P在EC的上方时,如图1,
则EF⊥BP,BE=PE,
∴∠PBE=∠BPE,
∵四边形ABCD是平行四边形,∠D=30°,
∴∠ABC=∠D=30°,
∵△PCE是等边三角形,
∴∠PEC=60°,
∵∠PEC=∠PBE+∠BPE,
∴∠PBE=30°,
∴∠ABC=∠PBC=30°,
∴B、F、A、P在同一直线上,
∴BF=BEcos30°=![]() =3.
=3.
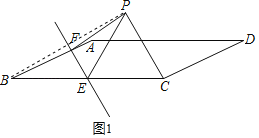
当点P在CE下方P′处时,如图2,连接BP′,
则EF′⊥BP′,BE=EP′,
∵△P′CE是等边三角形,
∴∠P′EC=60°,
∵∠P′EC=∠P′BE+∠BP′E,
∴∠P′BE=30°,
∴BQ=BEcos30°=2![]() =3,
=3,
∠ABP′=60°,
∴BF′=![]() =6,
=6,
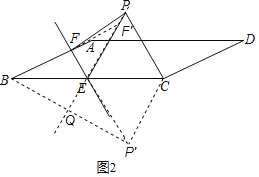
故答案为:3或6.

【题目】某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
电脑型号 | ① | ② | ③ |
工时(个) |
|
|
|
产值(万元) | 0.4 | 0.3 | 0.2 |
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
【题目】“莓好河南,幸福家园”,2019年某省草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,且推出了如下的优惠方案:
甲园 | 游客进园需购买20元/人的门票,采摘的草莓六折优惠 |
乙园 | 游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠 |
活动期间,小雪与爸爸妈妈决定选一个周末一同去采摘草莓,若设他们的草莓采摘量为x(千克)(出园时欲将自己采摘的草莓全部购买),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.

(1)求y1、y2与x之间的函数关系式;
(2)请在图中画出y1与x之间大致的函数图象;
(3)若小雪和爸爸妈妈当天所采摘的草莓不少于10千克,则选择哪个草莓园更划算?请说明理由.
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
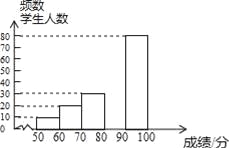
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?