题目内容
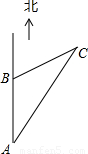
一艘轮船沿正北方向航行,在A处测得北偏东21.3°方向有一座小岛C,继续向北航行60海里到达B处,测得小岛C此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行多少海里,距离小岛C最近?
(参考数据:sin21.3°≈
,tan21.3°≈
,sin63.5°≈
,tan63.5°≈2)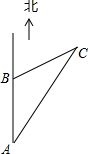
(参考数据:sin21.3°≈
| 9 |
| 25 |
| 2 |
| 5 |
| 9 |
| 10 |

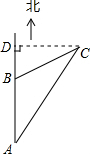
过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设BD=x海里,
在直角△BCD中,CD=BD?tan∠CBD=x?tan63.5°,
在直角△ACD中,AD=AB+BD=(60+x)海里,tan∠A=
| CD |
| AD |
∴CD=(60+x)?tan21.3°,
∴x?tan63.5°=(60+x)tan21.3°,
即2x=
| 2 |
| 5 |
解得:x=15,
答:轮船继续向北航行15海里,距离小岛C最近.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
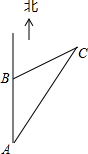 一艘轮船沿正北方向航行,在A处测得北偏东21.3°方向有一座小岛C,继续向北航行60海里到达B处,测得小岛C此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行多少海里,距离小岛C最近?
一艘轮船沿正北方向航行,在A处测得北偏东21.3°方向有一座小岛C,继续向北航行60海里到达B处,测得小岛C此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行多少海里,距离小岛C最近?
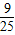 ,tan21.3°≈
,tan21.3°≈ ,sin63.5°≈
,sin63.5°≈ ,tan63.5°≈2)
,tan63.5°≈2)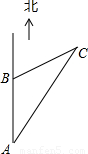
 ,tan21.3°≈
,tan21.3°≈ ,sin63.5°≈
,sin63.5°≈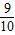 ,tan63.5°≈2)
,tan63.5°≈2)