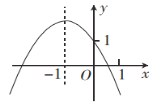题目内容
【题目】已知函数 (
(![]() 为常数)
为常数)
(1)当![]() ,
,
①点![]() 在此函数图象上,求
在此函数图象上,求![]() 的值;
的值;
②求此函数的最大值.
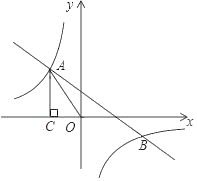
(2)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,当此函数的图象与线段
,当此函数的图象与线段![]() 只有一个交点时,直接写出
只有一个交点时,直接写出![]() 的取值范围.
的取值范围.
(3)当此函数图象上有4个点到![]() 轴的距离等于4,求
轴的距离等于4,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ②
②![]() ;(2)
;(2)![]() ,
,![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;(3)函数图象上有4个点到
只有一个交点;(3)函数图象上有4个点到![]() 轴的距离等于4时,
轴的距离等于4时,![]() 或
或![]() .
.
【解析】
(1)①将![]() 代入
代入![]() ;②当
;②当![]() 时,当
时,当![]() 时有最大值为5;当
时有最大值为5;当![]() 时,当
时,当![]() 时有最大值为
时有最大值为![]() ;故函数的最大值为
;故函数的最大值为![]() ;
;
(2)将点![]() 代入
代入![]() 中,得到
中,得到![]() ,所以
,所以![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;将点
只有一个交点;将点![]() )代入
)代入![]() 和
和![]() 中,得到
中,得到![]() ,
,
所以![]() 时图象与线段
时图象与线段![]() 只有一个交点;
只有一个交点;
(3)当![]() 时,
时,![]() ,得到
,得到![]() ;当
;当![]() 时,
时,![]() ,得到
,得到![]() ,当
,当![]() 时,
时,![]() ,
,![]() .
.
解:(1)当![]() 时,
时,
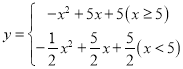 ,
,
①将![]() 代入
代入![]() ,
,
∴![]() ;
;
②当![]() 时,当
时,当![]() 时有最大值为5;
时有最大值为5;
当![]() 时,当
时,当![]() 时有最大值为
时有最大值为![]() ;
;
∴函数的最大值为![]() ;
;
(2)将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
∴![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;
只有一个交点;
将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
∴![]() 时图象与线段
时图象与线段![]() 只有一个交点;
只有一个交点;
综上所述:![]() ,
,![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;
只有一个交点;
(3)当![]() 时,
时,![]() ,
,
![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,
,
![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ;
;
∴函数图象上有4个点到![]() 轴的距离等于4时,
轴的距离等于4时,![]() 或
或![]() .
.

练习册系列答案
相关题目