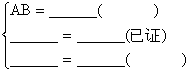题目内容
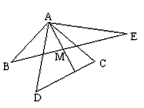
 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;解:∵∠1=∠2
已知
已知
∴∠1+∠EAB=∠2+∠EAB
即∠DAB=∠EAC
在△AEC和△ADB中
∵
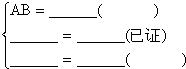
∴△AEC≌△ADB
SAS
SAS
∴CE=BD
(全等三角形对应边相等)
(全等三角形对应边相等)
.分析:根据全等三角形的判定以及书写格式填写理论依据即可.
解答:解:∵∠1=∠2(已知),
∴∠1+∠EAB=∠2+∠EAB,
即∠DAB=∠EAC,
在△AEC和△ADB中,
∵
,
∴△AEC≌△ADB(SAS),
∴CE=BD(全等三角形对应边相等).
故答案为:已知,AC,已知,∠DAB,∠EAC,AD,AE,已知,SAS,(全等三角形对应边相等).
∴∠1+∠EAB=∠2+∠EAB,
即∠DAB=∠EAC,
在△AEC和△ADB中,
∵
|
∴△AEC≌△ADB(SAS),
∴CE=BD(全等三角形对应边相等).
故答案为:已知,AC,已知,∠DAB,∠EAC,AD,AE,已知,SAS,(全等三角形对应边相等).
点评:本题考查了全等三角形的判定与性质,主要是练习同学们的证明书写格式以及推理理论依据的填写,是基础题,理清证明思路是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
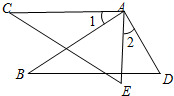 22、如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
22、如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程; 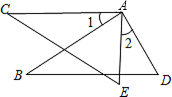 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程; 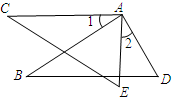 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;