题目内容
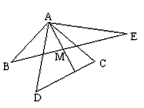
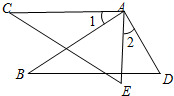 22、如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
22、如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程; 解:∵∠1=∠2(
已知
)∴∠1+∠EAB=∠2+∠EAB
即∠DAB=∠EAC
在△AEC和△ADB中
AC=AB,∠CAE=∠BAD,AE=AD,
∴△AEC≌△ADB(SAS)
∴CE=BD(
全等三角形的对应边相等
)分析:∠1=∠2已知,根据SAS得到△AEC≌△ADB,根据全等三角形的性质得到CE=BD,理由是全等三角形的对应边相等.
解答:解:∵∠1=∠2( 已知)
∴∠1+∠EAB=∠2+∠EAB
即∠DAB=∠EAC
在△AEC和△ADB中
AC=AB,∠CAE=∠BAD,AE=AD,
∴△AEC≌△ADB(SAS)
∴CE=BD( 全等三角形的对应边相等).
故答案为:已知,SAS,全等三角形的对应边相等.
∴∠1+∠EAB=∠2+∠EAB
即∠DAB=∠EAC
在△AEC和△ADB中
AC=AB,∠CAE=∠BAD,AE=AD,
∴△AEC≌△ADB(SAS)
∴CE=BD( 全等三角形的对应边相等).
故答案为:已知,SAS,全等三角形的对应边相等.
点评:本题主要考查对全等三角形的性质和判定,等式的性质等知识点的理解和掌握,解此题的关键是理解每一步的理由.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
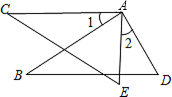 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程; 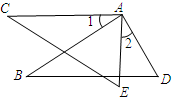 如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;
如图AB=AC,AD=AE,∠1=∠2,则CE=BD,完成下列推理过程;