题目内容
【题目】已知二次函数y=mx2+nx+p图象的顶点横坐标是2，与x轴交于A（x1，0）、B（x2，0），x1＜0＜x2，与y轴交于点C，O为坐标原点，tan∠CAO﹣tan∠CBO=1．
（1）求证：n+4m=0；
（2）求m、n的值；
（3）当p＞0且二次函数图象与直线y=x+3仅有一个交点时，求二次函数的最大值．
【答案】(1)证明见解析（2）m=
，n=-1或m=-
，n=1（3）4
【解析】
试题分析：（1）由题意可知抛物线的对称轴为x=2，利用对称轴公式x=
，易证n+4m=0；
（2）本问利用三角函数定义和抛物线与x轴交点坐标性质求解．特别需要注意的是抛物线的开口方向未定，所以所求m、n的值将有两组，不能遗漏；
（3）本问利用一元二次方程的判别式等于0求解．当p＞0时，m、n的值随之确定；将抛物线的解析式与直线的解析式联立，得到一个一元二次方程；由交点唯一可知，此一元二次方程的判别式等于0，据此求出p的值，从而确定了抛物线的解析式；最后由抛物线的解析式确定其最大值．
试题解析：
（1）∵二次函数y=mx2+nx+p图象的顶点横坐标是2，
∴抛物线的对称轴为x=2，
即
=2，
化简得：n+4m=0．
（2）∵二次函数y=mx2+nx+p与x轴交于A（x1，0）、B（x2，0），x1＜0＜x2，
∴OA=﹣x1，OB=x2；
x1+x2=
，x1x2=
；
令x=0，得y=p，
∴C（0，p），
∴OC=|p|．
由三角函数定义得：tan∠CAO=
，tan∠CBO=
．
∵tan∠CAO﹣tan∠CBO=1
，即
，
化简得：
=
，
将x1+x2=
，x1x2=
代入得：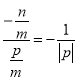
，
化简得：n=
=±1．
由（1）知n+4m=0，
∴当n=1时，m=-
；当n=﹣1时，m=
．
∴m、n的值为：m=
，n=﹣1（此时抛物线开口向上）或m=-
，n=1（此时抛物线开口向下）．
（3）解：由（2）知，当p＞0时，n=1，m=-
，
∴抛物线解析式为：y=
x2+x+p．
联立抛物线y=x2+x+p与直线y=x+3解析式得到： x2+x+p=x+3，
化简得：x2﹣4（p﹣3）=0 ①．
∵二次函数图象与直线y=x+3仅有一个交点，
∴一元二次方程①的判别式等于0，
即△=02+16（p﹣3）=0，解得p=3．
∴抛物线解析式为：y=x2+x+p=y=x2+x+3=（x﹣2）2+4，
当x=2时，二次函数有最大值，最大值为4．
∴当p＞0且二次函数图象与直线y=x+3仅有一个交点时，二次函数的最大值为4．
