题目内容
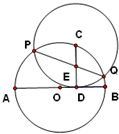
如图,已知AB为⊙O的弦,M为AB的中点,P为⊙O上任意一点,以点P为圆心、2MO为半径作圆并交⊙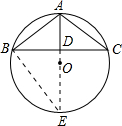 O于点C、D,AC、BD交于点Q,请问:
O于点C、D,AC、BD交于点Q,请问:
(1)点Q是△PAB的什么“心”?
(2)点Q是否在⊙P上?试证明你的结论.
提示:(1)三角形的三条高线交于一点,称为垂心定理,此点称为垂心.
(2)三角形有内心、外心、重心、垂心等.
 解:(1)如图,作⊙O的直径BE,连接OM、PD、DE、EA.
解:(1)如图,作⊙O的直径BE,连接OM、PD、DE、EA.∵BE为⊙O直径,
∴∠BAE=90°,
而M为AB的中点,所以OM⊥AB,
∴AE∥MO,AE=2MO.
而PD=2OM,
∴AE=PD,
∴∠DEP=∠EPA,
∴DE∥AP,
又∵∠BDE=90°,即BD⊥DE,
所以,BD⊥PA,
即点Q在△PAB的顶点B到底边PA的垂线上.
连接PE、PC.
同理可得AC⊥PB,即点Q在△PAB的顶点A到底边PB的垂线上.
∴Q是△PAB两条高的交点,
故Q为△PAB的垂心.
(2)点Q在⊙P上.
理由如下:
连接PQ.
∴PQ⊥AB,
而AE⊥AB,
∴PQ∥AE.
又∵PE∥AC,即有PE∥AQ,
∴四边形AQPE为平行四边形.
∴PQ=AE=PC=2MO.
故点Q在⊙P上.
分析:(1)作⊙O的直径BE,连接OM、PD、DE、EA.先由∠BAE=90°OM⊥AB,证明出AE=2MO.而PD=2OM,得AE=PD,得∠DEP=∠EPA,所以DE∥AP,而BD⊥DE,于是BD⊥PA,同理可得AC⊥PB,因此判断Q为△PAB的垂心.
(2)连接PQ.由PQ⊥AB,AE⊥AB,得PQ∥AE,而PE∥AC,得到四边形AQPE为平行四边形,所以PQ=AE=PC=2MO,故点Q在⊙P上.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度.也考查了三角形中位线的性质和平行线的性质.

练习册系列答案
相关题目
 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )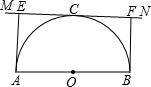 如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F.
如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F.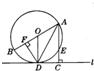 如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F.
如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F.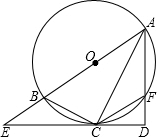 (2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.
(2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.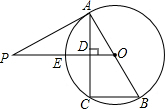 (2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.