题目内容
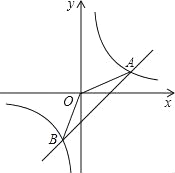
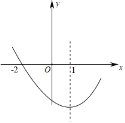
【题目】在平面直角坐标系xOy中,抛物线G:![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数
与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数![]() (
(![]() )的图像为直线
)的图像为直线![]() .
.
(1)求A、B两点的坐标;
(2)当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]() ,试说明:抛物线G的顶点不在直线
,试说明:抛物线G的顶点不在直线![]() 上;
上;
(3)设![]() ,直线
,直线![]() 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线
与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线![]() 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
【答案】(1)点A的坐标(-1,0),点B的坐标(3,0);(2)见解析;(3)4, 5,6,7,8
【解析】
(1)令![]() ,可解得A,B坐标;
,可解得A,B坐标;
(2)将![]() 配方为顶点式,得顶点坐标;确定1≤x≤2与对称轴的关系,表示出m,n的值;将顶点代入
配方为顶点式,得顶点坐标;确定1≤x≤2与对称轴的关系,表示出m,n的值;将顶点代入![]() 进行判断即可;
进行判断即可;
(3)当A、C两点到直线![]() 距离相等时,
距离相等时,![]() 过AC中点,确定直线
过AC中点,确定直线![]() ,表示点F坐标,确定点E坐标,求出BE所在直线的解析式,若F在BE上方,得不等式即可,求出n的取值范围,可得整数n.
,表示点F坐标,确定点E坐标,求出BE所在直线的解析式,若F在BE上方,得不等式即可,求出n的取值范围,可得整数n.
(1)令![]() ,得
,得![]() ,
,
即![]() ,解得
,解得![]()
∵A在B的左侧,
∴A(![]() ),B(3,0)
),B(3,0)
(2)由![]()
得顶点坐标为:(![]() ),对称轴为
),对称轴为![]()
∵![]() ,开口向下
,开口向下
∴当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]()
得![]() ,即
,即![]()
∴![]()
当![]() 时,
时,![]()
∴抛物线G的顶点不在直线![]() 上
上
(3)当![]() 时,
时,![]()
∴C(0,9)
∵A、C两点到直线![]() 距离相等
距离相等
∴直线![]() 过A,C两点的中点
过A,C两点的中点
∵A(![]() )
)
∴D(![]() )
)
将点D代入![]() 得:
得:![]() ,即
,即![]()
∴直线![]() 可化为:
可化为:![]()
∴E(0,![]() )
)
设BE的解析式为:![]()
则![]() ,解得
,解得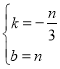
故BE的解析式为:![]()
∵点F为直线![]() 与对称轴交点
与对称轴交点
∴F(![]() )
)
又点F在直线BE上方
∴![]() ,解得
,解得![]()
又∵![]()
∴![]()
∵![]() 为整数
为整数
∴![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某超市为了回惯顾客,计划于周年店庆当天举行抽奖活动.凡是购物金额达到m元及以上的顾客,都将获得抽奖机会.规则如下:在一个不透明袋子里装有除数字标记外其它完全相同的4个小球,数字标记分别为“a” 、“b”、“c”、“0” (其中正整数a、b、c满足a+b+c=30且a>15).顾客先随机摸出一球后不放回,再摸出第二球,则两球标记的数字之和为该顾客所获奖励金额(单位:元)、经调查发现,每日前来购物的顾客中,购物金额及人数比例如下表所示:
购物金额x (单位:元) | 0<x<100 | 100≤x<200 | 200≤x<300 | x≥300 |
人数比例 |
|
|
|
|
现预计活动当天购物人数将达到200人.
(1)在活动当天,某顾客获得抽奖机会,试用画树状图或列表的方法,求该顾客获得a元奖励金的概率;
(2)以每位抽奖顾客所获奖励金的平均数为决策依据,超市设定奖励总金额不得超过2000元,且尽可能让更多的顾客参与抽奖活动,问m应定为100元?200元?还是300元?请说明理由.
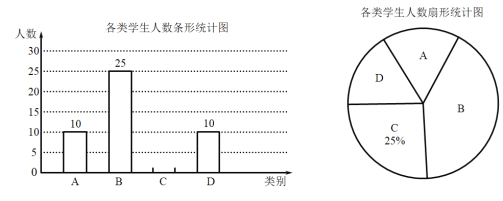
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?