题目内容
如图所示,直角梯形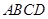 中,
中,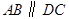 ,
,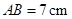 ,
,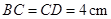 ,以
,以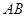 所在直线为轴旋转一周,得到一个几何体,求它的全面积.
所在直线为轴旋转一周,得到一个几何体,求它的全面积.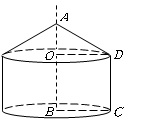
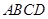 中,
中,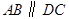 ,
,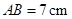 ,
,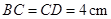 ,以
,以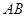 所在直线为轴旋转一周,得到一个几何体,求它的全面积.
所在直线为轴旋转一周,得到一个几何体,求它的全面积.
(8分)68Π
分析:所得几何体为圆锥和圆柱的组合图形,表面积为底面半径为4,母线长的平方等于42+32的圆锥的侧面积和底面半径为4,高为4的圆柱的侧面积和下底面积之和。
解答:
∵Rt△AOD中,AO=7-4=3cm,OD=4cm,
∴AD2=42+32=25
∴AD =5cm,
∴所得到的几何体的表面积为π×4×5+π×4×2×4+π×4×4=68πcm2。
故它的全面积为68πcm2。
点评:考查圆锥的计算和圆柱的计算;得到几何体的形状是解决本题的突破点;需掌握圆锥、圆柱侧面积的计算公式。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
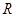 的长为
的长为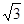 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为
cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为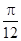
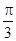
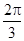
 ,cosB
,cosB .如果⊙O的半径为
.如果⊙O的半径为 cm,且经过点B、C,那么线段AO= cm.
cm,且经过点B、C,那么线段AO= cm.
 的直径,点C、D在
的直径,点C、D在 ,
, ,则
,则 ( )
( ) 的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为(
的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为( ,
, ).
). 相切,并求点P的坐标.
相切,并求点P的坐标.



