题目内容
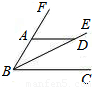
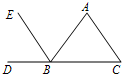17、如图，请你填写一个适当的条件：∠DBE=∠C或∠EBA=∠A或∠EBC+∠C=180°
，使BE∥AC．分析：根据平行线的判定定理，填写一个适当的条件，即可解答．
解答：解：①根据两条直线被第三条所截，如果同位角相等，那么这两条直线平行，
所以，∠DBE=∠C时，BE∥AC．
②两条直线被第三条所截，如果内错角相等，那么这两条直线平行，
所以，∠EBA=∠A时，BE∥AC．
③两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行，
所以，∠EBC+∠C=180°时，BE∥AC．
故答案为：∠DBE=∠C或∠EBA=∠A或∠EBC+∠C=180°．
所以，∠DBE=∠C时，BE∥AC．
②两条直线被第三条所截，如果内错角相等，那么这两条直线平行，
所以，∠EBA=∠A时，BE∥AC．
③两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行，
所以，∠EBC+∠C=180°时，BE∥AC．
故答案为：∠DBE=∠C或∠EBA=∠A或∠EBC+∠C=180°．
点评：本题考查了平行线的判定，此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放性题目，能有效地培养学生“执果索因”的思维方式与能力．
练习册系列答案
相关题目
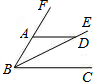3、如图，请你填写一个适当的条件：
11、如图，请你填写一个适当的条件：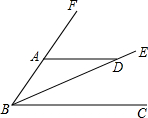
如图，①请你填写一个适当的条件：