题目内容
若在同一坐标系中，直线y=k1x与双曲线y=
无交点，则有（ ）
| k2 |
| x |
| A、k1+k2＞0 |
| B、k1+k2＜0 |
| C、k1k2＞0 |
| D、k1k2＜0 |
分析：因为直线y=k1x与双曲线y=
无交点，故由二者组成的方程组无解，相应的，解方程组时，消元后得到的一元二次方程无解，故可用一元二次方程根的判别式解答．
| k2 |
| x |
解答：解：因为直线y=k1x与双曲线y=
无交点，
故
无解；
即k1x=
，
于是k1x2=k2，
即是k1x2-k2=0无解，
于是△=02-4×k1（-k2）＜0，
整理得k1k2＜0．
故选D．
| k2 |
| x |
故
|
即k1x=
| k2 |
| x |
于是k1x2=k2，
即是k1x2-k2=0无解，
于是△=02-4×k1（-k2）＜0，
整理得k1k2＜0．
故选D．
点评：解答此题要将解析式组成方程组，判断出方程组解的个数，进而判断出交点的坐标的个数，体现了数形结合的思想．
练习册系列答案
相关题目
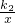无交点，则有
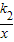无交点，则有（ ）
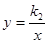无交点，则有（ ）