Question

（2005•西宁）2002年8月，在北京召开国际数学家大会，大会会标是由4个全等的直角三角形与一个小正方形拼成的大正方形（如图）．若大正方形的面积是32，小正方形的面积是4，则每个直角三角形的周长为    ．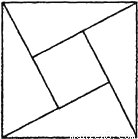

Answer 1

【答案】分析：设直角三角形的两条直角边分别是a，b，根据已知可列两个方程，由方程可求得直角三角形两直角边的和及其斜边的长，从而不难求得其周长．
解答：解：设直角三角形的两条直角边分别是a，b
根据题意，得a²+b²=32①
2ab=32-4=28②
①+②，得（a+b）²=60，
a+b=2，
由①，得直角三角形的斜边是4，
则每个直角三角形的周长是2+4．
点评：此题要根据图形的面积分别表示出直角三角形的直角边的关系式，然后结合完全平方公式求得两条直角边的和，进一步求得其周长．