题目内容
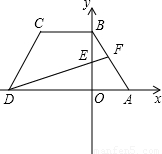
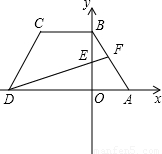
(2005•西宁)如图,在等腰梯形ABCD中,AD∥BC,BA=CD,AD的长为4,S梯形ABCD=9.已知点A、B的坐标分别为(1,0)和(0,3).(1)求点C的坐标;
(2)取点E(0,1),连接DE并延长交AB于P试猜想DF与AB之间的关系,并证明你的结论;
(3)将梯形ABCD绕点A旋转180°后成梯形AB′C′D′,求对称轴为直线x=3,且过A、B′两点的抛物线的解析式.
【答案】分析:(1)根据等腰三角形的性质,易得点C到X,Y轴的距离,进而可得C的坐标;
(2)根据三角函数的定义求出有tan∠FDA与tan∠BAO值,进而可得DF⊥AB;
(3)根据题意,设出其方程,将AB的坐标代入可得ac的值,化简可得抛物线解析式.
解答: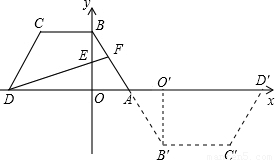 解:(1)根据题意,点A、B的坐标分别为(1,0)和(0,3)易得OB=3,BC=2,
解:(1)根据题意,点A、B的坐标分别为(1,0)和(0,3)易得OB=3,BC=2,
可得C到x轴的距离为3,到y轴的距离为2,
故C(-2,3).
(2)猜想:DF⊥AB.
根据题意,易得tan∠FDA= =
= ,
,
同时可得tan∠BAO=-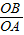 =-3,
=-3,
有tan∠FDA×tan∠BAO=-1,
故DF⊥AB.
(3)根据题意,设其方程为y=a(x-3)2+c,
同时有A(1,0),(5,0),
将其代入方程可得a=1,c=-4,
化简可得y=x2-6x+5,
故所求的抛物线解析式为y=x2-6x+5.
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.
(2)根据三角函数的定义求出有tan∠FDA与tan∠BAO值,进而可得DF⊥AB;
(3)根据题意,设出其方程,将AB的坐标代入可得ac的值,化简可得抛物线解析式.
解答:
 解:(1)根据题意,点A、B的坐标分别为(1,0)和(0,3)易得OB=3,BC=2,
解:(1)根据题意,点A、B的坐标分别为(1,0)和(0,3)易得OB=3,BC=2,可得C到x轴的距离为3,到y轴的距离为2,
故C(-2,3).
(2)猜想:DF⊥AB.
根据题意,易得tan∠FDA=
 =
= ,
,同时可得tan∠BAO=-
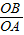 =-3,
=-3,有tan∠FDA×tan∠BAO=-1,
故DF⊥AB.
(3)根据题意,设其方程为y=a(x-3)2+c,
同时有A(1,0),(5,0),
将其代入方程可得a=1,c=-4,
化简可得y=x2-6x+5,
故所求的抛物线解析式为y=x2-6x+5.
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (2005•西宁)如图,在格点图中,l1、l2是两条互相垂直的直线.
(2005•西宁)如图,在格点图中,l1、l2是两条互相垂直的直线. cm,AB=6 cm,求∠ACB的度数.
cm,AB=6 cm,求∠ACB的度数.