题目内容
在△ABC中，已知∠A、∠B都是锐角，且sinA=
，tanB=1，则∠C的度数为（ ）A．75°
B．105°
C．60°
D．45°
【答案】分析：根据sinA=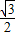
，∠A是锐角，可知∠A=60°，同理可得∠B=45°，结合三角形内角和定理可求∠C．
解答：解：∵sinA=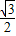
，∠A是锐角，
∴∠A=60°，
同理可得∠B=45°，
∴∠C=180°-60°-45°=75°，
故选A．
点评：本题考查了特殊三角函数值、三角形内角和定理，解题的关键是熟练掌握30°、60°、45°这些特殊角的特殊三角函数值．
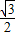，∠A是锐角，可知∠A=60°，同理可得∠B=45°，结合三角形内角和定理可求∠C．解答：解：∵sinA=
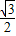，∠A是锐角，∴∠A=60°，
同理可得∠B=45°，
∴∠C=180°-60°-45°=75°，
故选A．
点评：本题考查了特殊三角函数值、三角形内角和定理，解题的关键是熟练掌握30°、60°、45°这些特殊角的特殊三角函数值．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
