题目内容
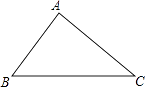
【题目】如图,在△AB C中,AB=AC,BD和CD分别是∠ABC和∠ACB的平分线,EF过D点,且EF∥BC,图中等腰三角形共有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
根据等腰三角形的判定定理,可以得出图中△ABC,△AEF,△DBC,△EBD,△FDC为等腰三角形.从而可以得出答案.
AB=AC,可知△ABC为等腰三角形;
∵FF∥BC,BD和CD分别是∠ABC和∠ACB的平分线
∴∠EDB=∠DBC,∠EBD=DBC
∴∠EDB=∠EBD,可知△EBD为等腰三角形;
同理可知△DFC为等腰三角形.
∵AB=AC,∴∠ABC=∠ACB,又BD和CD分别是∠ABC和∠ACB的平分线
∴∠DBC=∠DCB,可知△DBC为等腰三角形,可知△EBD与△DFC全等,所以BE=CF
∴AE=AF,故△AEF为等腰三角形.
故选D.

练习册系列答案
相关题目