题目内容
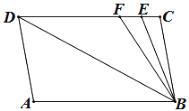
【题目】(1) 如图1,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF,四边形AEGF是矩形,写出矩形AEGF的面积y与BE的长x之间的函数关系式;
(2) 如图2,已知一长方形打印纸长20 cm,宽15 cm,现在要在打印纸上打印文稿,上下左右各留出一定距离.设留出的距离均为x cm,打印文稿面积为y cm2,试写出y与x之间的关系式,并求出x的取值范围.
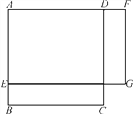
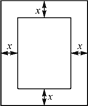
图1 图2
【答案】(1)y=25-x2(2)y=4x2-70x+300(0<x<7.5)
【解析】【试题分析】
(1)设BE=DF=x,则AE=5-x,AF=5+x.根据矩形的面积等于长乘以宽,即y=AE·AF=(5-x)(5+x)=25-x2;
(2)由题意得:打印的部分长为(20-2x)cm,宽为(15-2x)cm,则打印部分的面积为y=(20-2x)(15-2x)=4x2-70x+300,同时满足![]() 则x的范围为0<x<7.5.
则x的范围为0<x<7.5.
【试题解析】
(1)∵BE=x,∴AE=5-x,AF=5+x.
∴y=AE·AF=(5-x)(5+x)=25-x2.
(2)y=(20-2x)(15-2x)=4x2-70x+300(0<x<7.5).

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目