题目内容
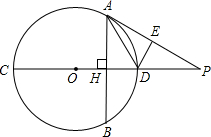 如图,AB为⊙O内垂直于直径的弦,AB、CD相于点H,△AED与△AHD关于直线AD成轴对称.
如图,AB为⊙O内垂直于直径的弦,AB、CD相于点H,△AED与△AHD关于直线AD成轴对称.(1)试说明:AE为⊙O的切线;
(2)延长AE与CD交于点P,已知PA=2,PD=1,求⊙O的半径和DE的长.
分析:(1)作辅助线OA构建平行线OA∥DE,然后由平行线的性质知∠OAP=90°;
(2)设⊙O的半径为x.在Rt△AOP中,利用勾股定理知OA2+AP2=OP2,然后将x代入其中,求得x=1.5;再来根据△PED∽△PAO的对应边成比例求得DE的长度即可.
(2)设⊙O的半径为x.在Rt△AOP中,利用勾股定理知OA2+AP2=OP2,然后将x代入其中,求得x=1.5;再来根据△PED∽△PAO的对应边成比例求得DE的长度即可.
解答: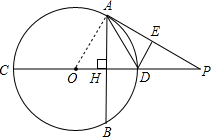 解:(1)连接OA.
解:(1)连接OA.
由△AED与△AHD关于直线AD成轴对称可知∠ADO=∠ADE,
∵AB⊥CD,
∴∠AED=∠AHD=90°.
又∵OA=OD(圆的半径),
∴∠OAD=∠ODA(等边对等角),
∴∠OAD=∠ADE(等量代换),
∴OA∥DE(内错角相等,两直线平行),
∴∠OAP=90°(两直线平行,同位角相等),
又∵点A在圆上,
∴AE为⊙O的切线;
(2)设⊙O的半径为x,在Rt△AOP中,
OA2+AP2=OP2
x2+22=(x+1)2(5分)
解得,x=1.5
∴⊙O的半径为1.5;
∵OA∥DE,
∴△PED∽△PAO
∴
=
,
=
,
解得DE=
.
 解:(1)连接OA.
解:(1)连接OA.由△AED与△AHD关于直线AD成轴对称可知∠ADO=∠ADE,
∵AB⊥CD,
∴∠AED=∠AHD=90°.
又∵OA=OD(圆的半径),
∴∠OAD=∠ODA(等边对等角),
∴∠OAD=∠ADE(等量代换),
∴OA∥DE(内错角相等,两直线平行),
∴∠OAP=90°(两直线平行,同位角相等),
又∵点A在圆上,
∴AE为⊙O的切线;
(2)设⊙O的半径为x,在Rt△AOP中,
OA2+AP2=OP2
x2+22=(x+1)2(5分)
解得,x=1.5
∴⊙O的半径为1.5;
∵OA∥DE,
∴△PED∽△PAO
∴
| DP |
| PO |
| DE |
| AO |
| 1 |
| 2.5 |
| DE |
| 1.5 |
解得DE=
| 3 |
| 5 |
点评:本题综合考查了切线的判定与性质、相似三角形的判定与性质、轴对称的性质及垂径定理.解答该题时,借助于辅助线OA,将隐含在题干中的条件半径OA∥DE浮于水面,降低了题的难度.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目


 21、某数学学习小组想利用旗杆上的绳子测量校园内旗杆AB的高度(如图,AB垂直地面BC).方法如下:先把旗杆绳(AD)垂下,测得绳子底端D距地面刚好1m.然后拉住绳子底端向外走7步(每步距离约为0.6 m),刚好能拉住绳子底端放在一高为1.6 m的同学头顶上,求旗杆AB的长.
21、某数学学习小组想利用旗杆上的绳子测量校园内旗杆AB的高度(如图,AB垂直地面BC).方法如下:先把旗杆绳(AD)垂下,测得绳子底端D距地面刚好1m.然后拉住绳子底端向外走7步(每步距离约为0.6 m),刚好能拉住绳子底端放在一高为1.6 m的同学头顶上,求旗杆AB的长. 如图,在同一平面内有A、B、C三个点,根据要求画图:
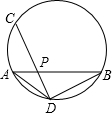
如图,在同一平面内有A、B、C三个点,根据要求画图: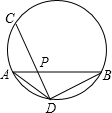
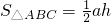 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.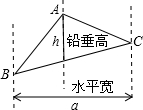
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.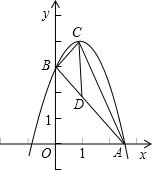
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.