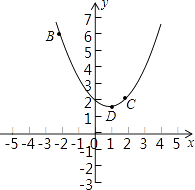Question

【题目】如图，Rt△AOB在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上,，将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.

（1）求直线BE的解析式;

（2）求点D的坐标;

（3）x轴上是否存在点P，使△PAD为等腰三角形？若存在，请直接写出点P的坐标，若不存在，请说明理由。

Answer 1

【答案】（1）y=x+2 （2）（-3，）（3） 或（）或（0,0）或（-4,0）

【解析】

（1）先利用直角三角形的性质（直角三角形中，如果有一个角是30°，那么它所对的直角边等于斜边的一半．）和勾股定理求出点的坐标E（﹣2，0），进一步用待定系数法求出一次函数的解析式y=x+2．

（2）过D作DG⊥OA于G．由折叠可知DE=2．再由∠EDG=30°，得到GE=1，DG=，从而可求出D的坐标；

（3）设P（x，0）．可求得DG=，AD=．然后分三种情况讨论：

①以A为圆心，AD为半径作圆与x轴交于点P；②以D为圆心，DA为半径作圆与x轴交于点P；③设线段AD的垂直平分线交x轴于P．

（1）∵OB=，AO=6，∴AB==，∴∠BAO=30°，∴∠ABO=60°．

∵沿BE折叠O、D重合，∴∠EBO=30°，OE=BE，设OE=x，则（2x）2=x2+，∴x=2，即 BE=4，E（﹣2，0），设y=kx+b代入得：，解得：，∴直线BE的解析式是：；

（2）过D作DG⊥OA于G．

∵沿BE折叠O、D重合，∴DE=2．

∵∠DAE=30°，∴∠DEA=60°，∠ADE=∠BOE=90°，∴∠EDG=30°，∴GE=1，DG=，∴OG=1+2=3，∴D的坐标是：D；

（3）设P（x，0）．

∵∠OAB=30°，DG=，∴AD=2DG=．分三种情况讨论：

①以A为圆心，AD为半径作圆与x轴交于点P，则AP=AD=，∴P(，0)；

②以D为圆心，DA为半径作圆与x轴交于点P，则AP=2AG= DG=6．

∵OA=6，∴P与O重合，∴P（0，0）；

③设线段AD的垂直平分线交x轴于P，则PA=PD，∴，解得：x=－4，∴P（－4，0）．

综上所述：P的坐标为：P(，0)或P（0，0）或P（－4，0）．