题目内容
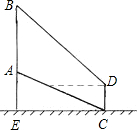 如图,山坡上(坡度i=1:
如图,山坡上(坡度i=1:| 3 |
| 3 |
分析:此题可先由坡角求得AC和AE的长,再由仰角求得BE的长,则树AB的高即可求出.
解答:解:由山坡的坡度i=1:
可得坡度角∠ACE=30°,
EC=40(米),AC=
=
≈46.19(米),
AE=EC•tan∠ACE=
≈23.10(米),
又在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,
则BE=CD+EC•tan45°=1.5+40=40.5(米),
AB=BE-AE=40.5-23.10≈17.40(米).
答:斜坡AC的长约为46.19米,树AB的高约为17.40米.
| 3 |
EC=40(米),AC=
| EC |
| cos∠ACE |
80
| ||
| 3 |
AE=EC•tan∠ACE=
40
| ||
| 3 |
又在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,
则BE=CD+EC•tan45°=1.5+40=40.5(米),
AB=BE-AE=40.5-23.10≈17.40(米).
答:斜坡AC的长约为46.19米,树AB的高约为17.40米.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
 如图,在一段坡度为1:2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为
如图,在一段坡度为1:2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为 (2012•抚顺一模)如图,小明在坡度为1:2.4的山坡AB上的A处测得大树CD顶端D的仰角为45°,CD垂直于水平面,测得坡面AB长为13米,BC长为9米,A、B、C、D在一个平面内,求树高CD.
(2012•抚顺一模)如图,小明在坡度为1:2.4的山坡AB上的A处测得大树CD顶端D的仰角为45°,CD垂直于水平面,测得坡面AB长为13米,BC长为9米,A、B、C、D在一个平面内,求树高CD. 如图,山坡上(坡度
如图,山坡上(坡度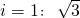 )有一棵树AB距山脚C处40米,小明在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,求斜坡AC的长和树AB的高.(
)有一棵树AB距山脚C处40米,小明在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,求斜坡AC的长和树AB的高.(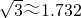 ,答案精确到0.01米)
,答案精确到0.01米) )有一棵树AB距山脚C处40米,小明在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,求斜坡AC的长和树AB的高.(
)有一棵树AB距山脚C处40米,小明在山脚C处用高为1.5米的测角仪CD测得树顶的仰角为45°,求斜坡AC的长和树AB的高.( ,答案精确到0.01米)
,答案精确到0.01米)