题目内容
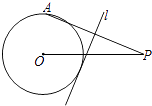
【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).
【答案】4π
【解析】解:顶点O经过的路线可以分为三段,
第一段:当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°.
此时点O经过了以O为圆心,以3为半径的圆的周长的 ![]() ,即经过了
,即经过了 ![]() ×2π×3=
×2π×3= ![]() ;
;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,
所以O与转动点的连线始终⊥直线l,
所以O点在水平运动,此时O点经过的路线长=BA’=AB的弧长= ![]() =π;
=π;
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°,
此时点O经过了以O为圆心,以3为半径的圆的周长的 ![]() ,即经过了
,即经过了 ![]() ×2π×3=
×2π×3= ![]() ;
;
所以,O点经过的路线总长S= ![]() +π+
+π+ ![]() =4π.
=4π.
所以答案是4π.
【考点精析】本题主要考查了圆心角、弧、弦的关系和弧长计算公式的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.

 名校课堂系列答案
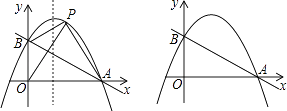
名校课堂系列答案【题目】已知:如图,∠MON=90°,△ABC中,∠C=90°,AC=3cm,BC=4cm,将△ABC的两个顶点A、B放在射线OM和ON上移动,作CD⊥ON于点D,记OA=x(当点O与A重合时,x的值为0),CD=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.

(1)通过取点、画图、计算、测量等方法,得到了x与y的几组值,如下表(补全表格)
x/cm | 0 | 1 | 2 | 3 | 4 | 4.5 | 5 |
y/cm | 2.4 | 3.0 | 3.5 | 3.9 | 4.0 | 3.9 |
|
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题;当x的值为 时,线段OC长度取得最大值为 cm.