题目内容
如图,把一边长为40cm的正方形硬纸板的四角各剪去一个同样大小的正方形,将剩余部分折成一个无盖的盒子.
(1)要使折成的盒子底面积为484cm2,那么剪掉的正方形边长为多少?
(2)折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形边长;如果没有,说明理由.

(1)要使折成的盒子底面积为484cm2,那么剪掉的正方形边长为多少?
(2)折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形边长;如果没有,说明理由.

分析:(1)利用已知图形利用边长与面积之间的关系得出解析式即可;
(2)利用长方形盒子的侧面积为:(40-2a)×a×4得出即可.
(2)利用长方形盒子的侧面积为:(40-2a)×a×4得出即可.
解答:解:(1)设减掉的正方形边长为xcm,根据题意得出:
(40-2x)(40-2x)=484,
解得:x1=9,x2=31(不合题意舍去),
答:剪掉的正方形边长为9cm;
(2)设减掉的正方形边长为ycm,
则长方形盒子的侧面积为:
S=4(40-2a)a
=-8a2+160a
=-8(a2-20a)
=-8(a-10)2+800,
∴当a=10时,S有最大值800,即则面积的最大值为800和此时剪掉的正方形边长为10cm.
(40-2x)(40-2x)=484,
解得:x1=9,x2=31(不合题意舍去),
答:剪掉的正方形边长为9cm;
(2)设减掉的正方形边长为ycm,
则长方形盒子的侧面积为:
S=4(40-2a)a
=-8a2+160a
=-8(a2-20a)
=-8(a-10)2+800,
∴当a=10时,S有最大值800,即则面积的最大值为800和此时剪掉的正方形边长为10cm.
点评:此题主要考查了二次函数的应用,利用已知得出剪掉的正方形边长与侧面积的函数关系式是解题关键.

练习册系列答案
相关题目
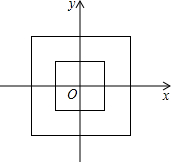 在平面直角坐标系中,我们把横、纵坐标都是整数的且互为相反数的两个点成为一组对称整点,观察如图所示的中心在原点、一边平行x轴的正方形,边长为1的正方形中没有对称整点;边长为2的正方形中有4组对称整点;边长为4的正方形中有12组对称整点,则边长为10的正方形中,对称整点的组数为( )
在平面直角坐标系中,我们把横、纵坐标都是整数的且互为相反数的两个点成为一组对称整点,观察如图所示的中心在原点、一边平行x轴的正方形,边长为1的正方形中没有对称整点;边长为2的正方形中有4组对称整点;边长为4的正方形中有12组对称整点,则边长为10的正方形中,对称整点的组数为( )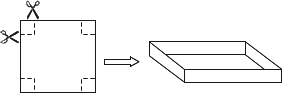
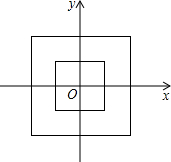 在平面直角坐标系中,我们把横、纵坐标都是整数的且互为相反数的两个点成为一组对称整点,观察如图所示的中心在原点、一边平行x轴的正方形,边长为1的正方形中没有对称整点;边长为2的正方形中有4组对称整点;边长为4的正方形中有12组对称整点,则边长为10的正方形中,对称整点的组数为
在平面直角坐标系中,我们把横、纵坐标都是整数的且互为相反数的两个点成为一组对称整点,观察如图所示的中心在原点、一边平行x轴的正方形,边长为1的正方形中没有对称整点;边长为2的正方形中有4组对称整点;边长为4的正方形中有12组对称整点,则边长为10的正方形中,对称整点的组数为