题目内容
 如图,B是线段AC上一点,△ABD与△BCE均为等边三角形.
如图,B是线段AC上一点,△ABD与△BCE均为等边三角形.(1)求证:AE=CD;
(2)若△BCE'与△BCE关于直线AC轴对称,AE'与CD还相等吗?画出图形.若相等,请给出证明;若不相等,说明理由;
(3)AE'与BD相交于点F,CD与BE'相交于点G,连接FG,试判断△FBG的形状,并加以证明.
分析:(1)易证△ABE≌△DBC,即可证得AE=CD;
(2)易知点E和E′关于直线AC轴对称,则可得AE=AE′,即可得出;
(3)由AE=DC,得∠EAD=∠CDA,则∠BAE=∠BDC,又∠BAE=∠BAE′,则可得∠BAE′=∠BDC,易得∠DBG=60°,易证△ABF≌△DBG,则可得FB=GB,所以,可得△FBG为等边三角形;
(2)易知点E和E′关于直线AC轴对称,则可得AE=AE′,即可得出;
(3)由AE=DC,得∠EAD=∠CDA,则∠BAE=∠BDC,又∠BAE=∠BAE′,则可得∠BAE′=∠BDC,易得∠DBG=60°,易证△ABF≌△DBG,则可得FB=GB,所以,可得△FBG为等边三角形;
解答:证明:(1)∵△ABD与△BCE均为等边三角形,
∴在△ABE和△DBC中,
,
∴△ABE≌△DBC,
∴AE=CD;
(2)∵△BCE'与△BCE关于直线AC轴对称,
∴点E和E′关于直线AC轴对称,
∴AE=AE′,又AE=AE′,
∴AE'=CD;
(3)∵△ABD与△BCE′均为等边三角形,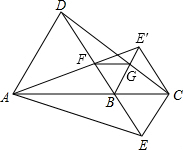
∴∠ABD=∠CBE′=60°,
∴∠DBE′=60°,
∵AE=DC,
∴∠EAD=∠CDA,
∴∠BAE=∠BDC,又∠BAE=∠BAE′,
∴∠BAE′=∠BDC,
在△ABF和△DBG中,
,
∴△ABF≌△DBG,
∴BF=BG,
∴△FBG为等边三角形.
∴在△ABE和△DBC中,
|
∴△ABE≌△DBC,
∴AE=CD;
(2)∵△BCE'与△BCE关于直线AC轴对称,
∴点E和E′关于直线AC轴对称,
∴AE=AE′,又AE=AE′,
∴AE'=CD;
(3)∵△ABD与△BCE′均为等边三角形,

∴∠ABD=∠CBE′=60°,
∴∠DBE′=60°,
∵AE=DC,
∴∠EAD=∠CDA,
∴∠BAE=∠BDC,又∠BAE=∠BAE′,
∴∠BAE′=∠BDC,
在△ABF和△DBG中,
|
∴△ABF≌△DBG,
∴BF=BG,
∴△FBG为等边三角形.
点评:本题主要考查了等边三角形的性质、全等三角形的判定与性质和轴对称图形的性质,注意正确画出图形,培养了学生综合运用知识解决问题的能力.

练习册系列答案
相关题目
 13、如图,B是线段AC上的一点,且AB:AC=2:5,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为
13、如图,B是线段AC上的一点,且AB:AC=2:5,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为 22、如图,B是线段AC上的一点,分别以AB、BC、AC为直径作半圆.过B作BD⊥AC,与较大半圆相交于点D,以BD为直径的圆交两个较小半圆于E、F.
22、如图,B是线段AC上的一点,分别以AB、BC、AC为直径作半圆.过B作BD⊥AC,与较大半圆相交于点D,以BD为直径的圆交两个较小半圆于E、F. 24、如图,B是线段AC上一点,△ABD和△BCE均为等边三角形.
24、如图,B是线段AC上一点,△ABD和△BCE均为等边三角形.