Question

24、如图，B是线段AC上一点，△ABD和△BCE均为等边三角形．
（1）求证：AE=CD．
（2）若△BCE与△BCE′关于直线AC轴对称，A E′与CD还相等吗？用尺规画出图形，若相等，请给出证明，若不相等请说明理由．

Answer 1

分析：（1）由已知，△ABD和△BCE均为等边三角形，得BE=BC，AB=BD，∠ABD=∠CBE=60°可得∠DBC=∠ABE，推出△ABE≌△DBC得证．
（2）先用尺规画出图形，由等边三角形证明△ABE^′≌△CBD．

解答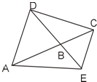：证：（1）∵△ABD和△BCE均为等边三角形
∴∠ABD=∠CBE=60^o，BE=BC，AB=BD
∴∠DBC=∠ABE=180^o-60^o=120^o
∴△ABE≌△DBC，
∴AE=CD．

（2）尺规作图如图
∵△ABD与△BCE'均为等边三角形
∴∠ABD=∠CBE'=60^o
AB=BD，BC=BE'
∴∠ABD=∠CBE'=60^o
AB=BD，BC=BE'
∴∠ABE'=∠ABD+∠DBE'
=∠CBE'+∠DBE'
=∠CBD
∴△ABE'≌△CBD，
∴AE'=CD

点评：此题考查的知识点是等边三角形的性质、全等三角形的判定与性质及轴对称的性质．关键是运用等边三角形的性质通过证明三角形全等得出．