题目内容
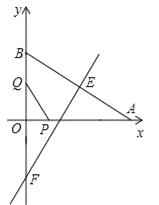
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )
①AC⊥DE;②![]() =
=![]() ;③CD=2DH;④
;③CD=2DH;④![]() .
.

A.1B.2C.3D.4
【答案】C
【解析】
试题分析:∵AD∥BC,∠ABC=90°
∴∠BAD=90°,
又∵AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,
∴AH⊥ED,
即AC⊥ED,故①正确;
∵△CHE为直角三角形,且∠HEC=60°
∴EC=2EH
∵∠ECB=15°,
∴EC≠4EB,
∴EH≠2EB;故②错误.
∵由证①中已知,∠BAC=∠CAD,
在△ACD和△ACE中,
 ,
,
∴△ACD≌△ACE(SAS),
∴CD=CE,
∵∠BCE=15°,
∴∠BEC=90°﹣∠BCE=90°﹣15°=75°,
∴∠CED=180°﹣∠BEC﹣∠AED=180°﹣75°﹣45°=60°,
∴△CDE为等边三角形,
∴∠DCH=30°,
∴CD=2DH,故③正确;
过H作HM⊥AB于M,
∴HM∥BC,
∴△AMH∽△ABC,
∴![]() ,
,
∵∠DAC=∠ADH=45°,
∴DH=AH,
∴![]() ,
,
∵△BEH和△CBE有公共底BE,
∴![]() ,故④正确,
,故④正确,
∴结论正确的个数是3.
故选C.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目