题目内容
 如图,已知AB是半圆O的直径,∠DAC=27°,D是弧AC的中点,那么∠BAC的度数是( )
如图,已知AB是半圆O的直径,∠DAC=27°,D是弧AC的中点,那么∠BAC的度数是( )分析:首先连接BC,由∠DAC=27°,D是弧AC的中点,可得AD=CD,可求得∠ACD的度数,继而求得∠D的度数,又由圆的内接四边形的性质,可求得∠B的度数,由AB是半圆O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,继而求得∠BAC的度数.
解答: 解:连接BC,
解:连接BC,
∵D是弧AC的中点,
∴AD=CD,
∴∠ACD=∠DAC=27°,
∴∠D=180°-∠DAC-∠ACD=126°,
∴∠B=180°-∠D=54°,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC=90°-∠B=36°.
故选B.
 解:连接BC,
解:连接BC,∵D是弧AC的中点,
∴AD=CD,
∴∠ACD=∠DAC=27°,
∴∠D=180°-∠DAC-∠ACD=126°,
∴∠B=180°-∠D=54°,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC=90°-∠B=36°.
故选B.
点评:此题考查了圆周角定理、圆的内接四边形的性质以及弧与弦的关系.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
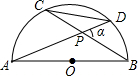 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )
如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
 如图,已知AB是半圆O的直径,∠BAC=32°,D是
如图,已知AB是半圆O的直径,∠BAC=32°,D是 |
| AC |
| A、25° | B、29° |
| C、30° | D、32° |
 如图,已知AB是半圆的直径,∠BAC=20°,D是
如图,已知AB是半圆的直径,∠BAC=20°,D是 (2012•葫芦岛一模)如图,已知AB是半圆O的直径,AB=10,点P是半圆周上一点,连接AP、BP,并延长BP至点C,使CP=BP,过点C作CE⊥AB,点E为垂足,CE交AP于点F,连接OF.
(2012•葫芦岛一模)如图,已知AB是半圆O的直径,AB=10,点P是半圆周上一点,连接AP、BP,并延长BP至点C,使CP=BP,过点C作CE⊥AB,点E为垂足,CE交AP于点F,连接OF.