Question

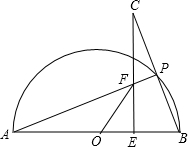（2012•葫芦岛一模）如图，已知AB是半圆O的直径，AB=10，点P是半圆周上一点，连接AP、BP，并延长BP至点C，使CP=BP，过点C作CE⊥AB，点E为垂足，CE交AP于点F，连接OF．
（1）当∠BAP=30°时，求

BP

的长度；
（2）当CE=8时，求线段EF的长；
（3）在点P运动过程中，点E随之运动到点A、O之间时，以点E、O、F为顶点的三角形与△BAP相似，请求出此时AE的长度．

Answer 1

分析：（1）连接OP，利用圆周角定理可得出∠BOP=2∠BAP，然后代入弧长公式即可求出

BP

的长度．
（2）连接AC，则可判断AP是线段BC的垂直平分线，在Rt△ACE中，求出AE，从而得出BE，再由Rt△AEF∽Rt△CEB，利用相似三角形的性质即可得出EF的长度．
（3）若以点E、O、F为顶点的三角形与△BAP相似，则有∠EOF=∠PAB或∠EOF=∠ABP，然后分别求出AE的长度即可．

解答：解：（1）连接OP，

∵AB=10，
∴OB=5，
又∵∠BAP=30°，
∴∠BOP=60°，
∴

BP

=

60×π×5

180

=

5π

3

．
（2）连接AC，

∵AB是半圆O的直径，
∴∠APB=90°，
又∵CP=BP，
∴AP是线段BC的垂直平分线，
∴AC=AB=10，
在Rt△ACE中，AE=

AC2-CE2

=

102-82

=6，
∴BE=4，
又∵Rt△AEF∽Rt△CEB，
∴

EF

BE

=

AE

CE

，

EF

4

=

6

8

，
∴EF=3．
（3）若以点E、O、F为顶点的三角形与△BAP相似，则有∠EOF=∠PAB或∠EOF=∠ABP，
①当∠EOF=∠PAB时，此时△AOF为等腰三角形，点E为AO的中点，即AE=

5

2

；
②当∠EOF=∠ABP时，OF∥BP，
此时OE=5-AE，BE=10-AE，
∵Rt△EOF∽Rt△EBC，
∴

OE

EB

=

OF

BC

，

5-AE

10-AE

=

1

4

，
∴AE=

10

3

．

点评：此题属于二次函数的综合题，涉及了圆周角定理、勾股定理、相似三角形的判定与性质，本题的难点在第三问，注意分类讨论，不要漏解，难度较大．