题目内容
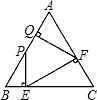 已知,如图,等边三角形ABC中,AB=4,点P为AB边上的任意一点(点P可以与点A重合,但不与点B重合),过点P作PE⊥BC,垂足为E,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q,设BP=x,AQ=y.
已知,如图,等边三角形ABC中,AB=4,点P为AB边上的任意一点(点P可以与点A重合,但不与点B重合),过点P作PE⊥BC,垂足为E,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q,设BP=x,AQ=y.
(1)写出y与x之间的函数关系式;
(2)当BP的长等于多少时,点P与点Q重合.
解:(1)PE⊥BC,EF⊥AC,FQ⊥AB,
∠A=∠B=∠C=60°,设BP=x,
∴BE= ,EC=4-
,EC=4- ,CF=2-
,CF=2- ,
,
AF=4-2+ =2+
=2+ ,
,
∵△BEP∽△AQF,
∴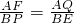 ,
,
∴AQ=1+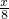 ,
,
∴y=1+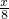 (0<x≤4);
(0<x≤4);
(2)当x+y=4,x+1+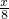 =4,
=4,
∴ x=3,
x=3,
∴x= .
.
故BP为 时,P与Q重合.
时,P与Q重合.
分析:(1)设BP=x,利用等边三角形中,三个角均为60°,三边长相等,逐步求出BE,EC,CF,AF的长,利用△BEP∽△AQF,对应边成比例,求出AP与AQ之间的关系;
(2)点P与点Q重合时,有AQ+AP=AB,代入关系式求解.
点评:解题的关键是利用锐角三角函数的概念,逐步找到x与y关系.
∠A=∠B=∠C=60°,设BP=x,
∴BE=
 ,EC=4-
,EC=4- ,CF=2-
,CF=2- ,
,AF=4-2+
 =2+
=2+ ,
,∵△BEP∽△AQF,
∴
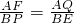 ,
,∴AQ=1+
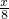 ,
,∴y=1+
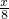 (0<x≤4);
(0<x≤4);(2)当x+y=4,x+1+
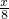 =4,
=4,∴
 x=3,
x=3,∴x=
 .
.故BP为
 时,P与Q重合.
时,P与Q重合.分析:(1)设BP=x,利用等边三角形中,三个角均为60°,三边长相等,逐步求出BE,EC,CF,AF的长,利用△BEP∽△AQF,对应边成比例,求出AP与AQ之间的关系;
(2)点P与点Q重合时,有AQ+AP=AB,代入关系式求解.
点评:解题的关键是利用锐角三角函数的概念,逐步找到x与y关系.

练习册系列答案
相关题目
 类似地你可以得到:“满足
类似地你可以得到:“满足
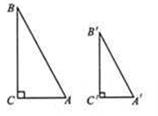
 ,则等边三角
,则等边三角
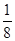 B.
B.  C.
C.
 D.1
D.1