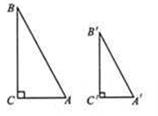
题目内容
学习《图形的相似》后，我们可以借助探索两个直角三角形全等的条件所获得经验，继续探索两个直角三角形相似的条件．（1）“对与两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”．
类似地你可以得到：“满足（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地你可以得到“满足
请结合下列所给图形，写出已知，并完成说理过程．
已知：如图，
试说明Rt△ABC∽Rt△A′B′C′．
分析：列举法证Rt△ABC∽Rt△A′B′C′；
可设AB、A′B′，AC、A′C′的比为k，进而由勾股定理求出BC：B′C′的值，此时可得两三角形的三边都对应成比例，由此来得出两三角形相似的结论．
可设AB、A′B′，AC、A′C′的比为k，进而由勾股定理求出BC：B′C′的值，此时可得两三角形的三边都对应成比例，由此来得出两三角形相似的结论．
解答：解：（1）一个锐角对应相等（1分）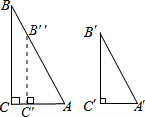
两直角边对应成比例（2分）
（2）斜边和一条直角边对应成比例（3分）
在AB上截取AC″=AC′，过C″作C″B″∥BC交AB于B″，
在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，
=
（4分）
解：设
=
=k，则AB=kA′B′，AC=kA′C′；
在Rt△ABC和Rt△A′B′C′中，
=
=
=k
∴
=
=
∴Rt△ABC∽Rt△A′B′C′．（8分）
两直角边对应成比例（2分）
（2）斜边和一条直角边对应成比例（3分）
在AB上截取AC″=AC′，过C″作C″B″∥BC交AB于B″，
在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，
| AB |
| A′B′ |
| AC |
| A′C′ |
解：设
| AB |
| A′B′ |
| AC |
| A′C′ |
在Rt△ABC和Rt△A′B′C′中，
| BC |
| B′C′ |
|
|
∴
| AB |
| A′B′ |
| AC |
| A′C′ |
| BC |
| B′C′ |
∴Rt△ABC∽Rt△A′B′C′．（8分）
点评：此题考查的是相似三角形的判定以及全等三角形的判定和性质．能够正确的理解材料的含义，熟练掌握相似三角形的判定方法是解答此题的关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
