Question

【题目】如图，以正六边形的对角线为边，向右作等边三角形，若四边形的面积为4，则五边形的面积为（ ）

A.6B.8C.10D.12

Answer 1

【答案】C

【解析】

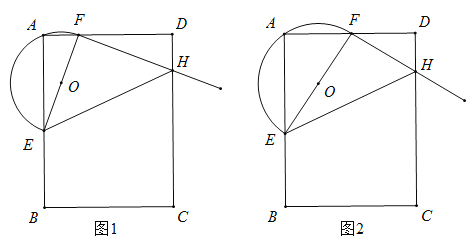
连接GC并延长交BD于点H，连接AE，根据正六边形和等边三角形的性质可得，△BCG≌△DCG，△GBC≌△DBC，所以得S△BCG=S△DCG=S△BCD=2，S△AEF=2，进而可得五边形ABDEF的面积．

解：如图，连接GC并延长交BD于点H，连接AE，

∵ABCDEF正六边形，
∴AB=BC=CD=DE=EF=AF，
∠F=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°，
∵△BDG是等边三角形，
∴BG=DG=BD
又CG=CG，
∴△BCG≌△DCG（SSS），
∵∠GBC=∠DBC=30°，
∴△GBC≌△DBC（SAS），
∴S△BCG=S△DCG=S△BCD=2，
∴S△AEF=2，
设CH=x，则BC=CG=2x，BH=，
∴BD=，
∴CGBH=2，
即×2x×=2，
∴，
∴S四边形ABDE=ABBD=2x2=4=8，
∴五边形ABDEF的面积为：2+8=10．
故选：C．