题目内容
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
【答案】(1)A奖品的单价是10元,B奖品的单价是15元;(2)应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
【解析】
试题分析:(1)设A奖品的单价是x元,B奖品的单价是y元,根据条件建立方程组求出其解即可;
(2)根据总费用=两种奖品的费用之和表示出W与m的关系式,并有条件建立不等式组求出x的取值范围,由一次函数的性质就可以求出结论.
试题解析:(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
![]() ,
,
解得:![]() .
.
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
W=10m+15(100-m)=-5m+1500
∴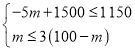 ,
,
解得:70≤m≤75.
∵m是整数,
∴m=70,71,72,73,74,75.
∵W=-5m+1500,
∴k=-5<0,
∴W随m的增大而减小,
∴m=75时,W最小=1125.
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目