题目内容
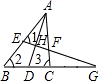如图，三角形ABC中，AD平分∠BAC，EG⊥AD，且分别交AB、AD、AC及BC的延长线于点E、H、F、G，下列四个式子中正确的是
- A.∠1=
（∠2-∠3） - B.∠1=2（∠2-∠3）
- C.∠G=（∠3-∠2）
- D.∠G=∠1
C
分析：根据角平分线得，∠1=∠AFE，由外角的性质，∠3=∠G+∠CFG=∠G+∠1，∠1=∠2+∠G，从而推得∠G=（∠3-∠2）．
解答：∵AD平分∠BAC，EG⊥AD，∴∠1=∠AFE，
∵∠3=∠G+∠CFG，∠1=∠2+∠G，∠CFG=∠AFE，
∴∠3=∠G+∠2+∠G，∠G=（∠3-∠2）．
故选C．
点评：本题考查了角平分线的定义以及多次利用外角的性质．
分析：根据角平分线得，∠1=∠AFE，由外角的性质，∠3=∠G+∠CFG=∠G+∠1，∠1=∠2+∠G，从而推得∠G=
（∠3-∠2）．解答：∵AD平分∠BAC，EG⊥AD，∴∠1=∠AFE，
∵∠3=∠G+∠CFG，∠1=∠2+∠G，∠CFG=∠AFE，
∴∠3=∠G+∠2+∠G，∠G=
（∠3-∠2）．故选C．
点评：本题考查了角平分线的定义以及多次利用外角的性质．
练习册系列答案
相关题目
16、如图，三角形ABC中，∠C=90°，它的三边AB、AC、BC中，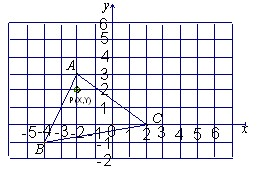
15、如图，三角形ABC中任意一点P（x，y），经过平移后对应的点Q（x+5，y+3），将三角形ABC作同样的平移到三角形A1B1C1．
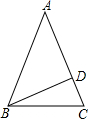已知：如图等腰三角形ABC中，AB=AC，BD平分∠ABC交AC于D，若∠BDC=78°，求∠C的度数？
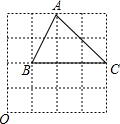如图，三角形ABC中，顶点B的位置表示为（1，2），点A的位置表示为（2，4）．则点C表示位置为
画图并计算，在如图的三角形ABC中：