ЬтФПФкШн
ЁОЬтФПЁПЁОдФЖСРэНтЁП
ЮвУЧжЊЕР1+2+3+Ё+n= ![]() ЃЌФЧУД12+22+32+Ё+n2НсЙћЕШгкЖрЩйФиЃП
ЃЌФЧУД12+22+32+Ё+n2НсЙћЕШгкЖрЩйФиЃП
дкЭМ1ЫљЪОШ§НЧаЮЪ§еѓжаЃЌЕк1аадВШІжаЕФЪ§ЮЊ1ЃЌМД12 ЃЌ Ек2ааСНИідВШІжаЪ§ЕФКЭЮЊ2+2ЃЌМД22 ЃЌ ЁЃЛЕк nаа nИідВШІжаЪ§ЕФКЭЮЊ ![]() ЃЌМДn2 ЃЌетбљЃЌИУШ§НЧаЮЪ§еѓжаЙВга
ЃЌМДn2 ЃЌетбљЃЌИУШ§НЧаЮЪ§еѓжаЙВга ![]() ИідВШІЃЌЫљгадВШІжаЪ§ЕФКЭЮЊ1+2+3+Ё+n2.
ИідВШІЃЌЫљгадВШІжаЪ§ЕФКЭЮЊ1+2+3+Ё+n2.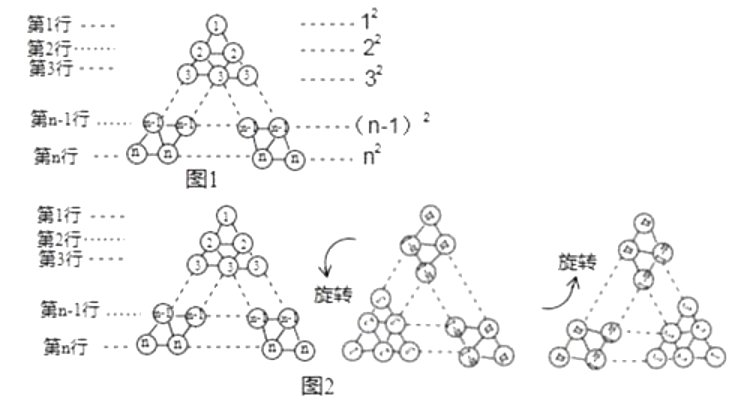
ЃЈ1ЃЉЁОЙцТЩЬНОПЁП
НЋШ§НЧаЮЪ§еѓОСНДЮа§зЊПЩЕУШчЭМ 2 ЫљЪОЕФШ§НЧаЮЪ§еѓЃЌЙлВьетШ§ИіШ§НЧаЮЪ§еѓИїааЭЌвЛЮЛжУдВШІжаЕФЪ§ЃЈШчЕк nЉ1ааЕФЕквЛИідВШІжаЕФЪ§ЗжБ№ЮЊ nЉ1ЃЌ2ЃЌnЃЉЃЌЗЂЯжУПИіЮЛжУЩЯШ§ИідВШІжаЪ§ЕФКЭОљЮЊ ЃЌ гЩДЫПЩЕУЃЌетШ§ИіШ§НЧаЮЪ§еѓЫљгадВШІжаЪ§ЕФзмКЭЮЊ3ЃЈ12+22+32+Ё+n2ЃЉ= ЃЌ вђДЫ12+22+32+Ё+n2=ЁЃ
ЃЈ2ЃЉЁОНтОіЮЪЬтЁП
ИљОнвдЩЯЗЂЯжЃЌМЦЫуЃК ![]()
ЁОД№АИЁП
ЃЈ1ЃЉ2n+1,(2n+1) ![]() ,
,![]()
ЃЈ2ЃЉНтЃКгЩЃЈ1ЃЉИіЙцТЩЕУЃК
дЪН= 
ЁОНтЮіЁПНтЃКЃЈ1ЃЉгЩЬтПЩжЊЃКУПИіЮЛжУЩЯдВШІжаЪ§ЕФКЭОљЮЊЃКn-1+2+n=2n+1ЃЌ
ЁретШ§ИіШ§НЧаЮЪ§еѓЫљгадВШІжаЪ§ЕФзмКЭЮЊ3ЃЈ12+22+32+Ё+n2ЃЉ=ЃЈ2n+1ЃЉЁСЃЈ1+2+3ЁЁ+nЃЉ
=ЃЈ2n+1ЃЉЁС![]() .
.
Ёр12+22+32+Ё+n2=![]() .
.
ЫљвдД№АИЪЧЃК2n+1ЃЌЃЈ2n+1ЃЉЁС![]() ЃЌ
ЃЌ![]()
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЪ§гыЪНЕФЙцТЩЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеЯШДгЭМаЮЩЯбАевЙцТЩЃЌШЛКѓбщжЄЙцТЩЃЌгІгУЙцТЩЃЌМДЪ§аЮНсКЯбАевЙцТЩВХФме§ШЗНтД№ДЫЬтЃЎ

