题目内容
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.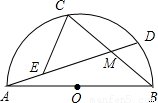
A.AB
B.CE
C.AM
D.CM
【答案】分析:连接BD,CD,利用同弧所对的圆周角相等得到∠B=∠ADC,再由已知的∠CEM=∠B,利用等量代换得到一对角相等,利用等角对等边得到CE=CD,由AB为圆O的直径,利用直径所对的圆周角为直角得到∠ADB=90°,在直角三角形BDM中,利用锐角三角函数定义表示出cos∠DMB,由对顶角相等得到cos∠DMB=cos∠AMC,再由∠B=∠ADC及一对对顶角相等,利用两对对应角相等的两三角形相似,得到三角形CMD与三角形ABM相似,由相似得比例,可得出CD:AB即为cos∠AMC的值,将AB=1,CD=CE代入即可得到其值为CE,得到正确的选项.
解答: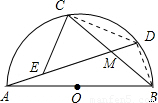 解:连接BD,CD,如图所示:
解:连接BD,CD,如图所示:
∵∠B和∠ADC都对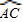 ,
,
∴∠B=∠ADC,又∠CEM=∠B,
∴∠CEM=∠ADC,
∴CE=CD,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△MBD中,cos∠DMB=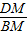 ,
,
∵∠AMC=∠DMB,
∴cos∠AMC=cos∠DMB=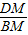 ,
,
∵∠ADC=∠B,∠CMD=∠AMB,
∴△CMD∽△AMB,
∴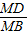 =
=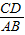 ,又AB=1,
,又AB=1,
∴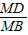 =CD,又CD=CE,
=CD,又CD=CE,
则cos∠AMC=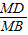 =CE.
=CE.
故选B
点评:此题考查了相似三角形的判定与性质,锐角三角函数定义,等腰三角形的判定,以及圆周角定理,熟练掌握相似三角形的判定与性质是解本题的关键.
解答:
 解:连接BD,CD,如图所示:
解:连接BD,CD,如图所示:∵∠B和∠ADC都对
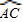 ,
,∴∠B=∠ADC,又∠CEM=∠B,
∴∠CEM=∠ADC,
∴CE=CD,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△MBD中,cos∠DMB=
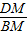 ,
,∵∠AMC=∠DMB,
∴cos∠AMC=cos∠DMB=
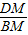 ,
,∵∠ADC=∠B,∠CMD=∠AMB,
∴△CMD∽△AMB,
∴
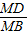 =
=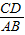 ,又AB=1,
,又AB=1,∴
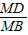 =CD,又CD=CE,
=CD,又CD=CE,则cos∠AMC=
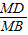 =CE.
=CE.故选B
点评:此题考查了相似三角形的判定与性质,锐角三角函数定义,等腰三角形的判定,以及圆周角定理,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
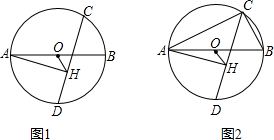
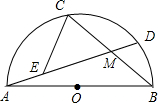 已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.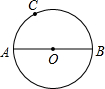 如图,已知AB为⊙O的直径,点C为半圆上的三等分点,在直径AB所在的直线上找一点P,连接CP交⊙O于点Q,使PQ=OQ,则∠CPO=
如图,已知AB为⊙O的直径,点C为半圆上的三等分点,在直径AB所在的直线上找一点P,连接CP交⊙O于点Q,使PQ=OQ,则∠CPO=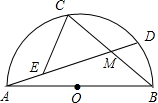 已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段的长.
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段的长.