题目内容
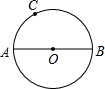如图，已知AB为⊙O的直径，点C为半圆上的三等分点，在直径AB所在的直线上找一点P，连接CP交⊙O于点Q，使PQ=OQ，则∠CPO=20°或40°或100°
20°或40°或100°
．分析：已知如图，连接OC，根据条件可得：∠A0C=60°，设∠CPO=x°，由隐藏条件：OQ=OC可得∠OCQ=∠CQO，再利用三角形外角和定理可建立关于x的方程，求出x的值即可得问题答案，本题还有其他两种情况，解答过程同上．
解答：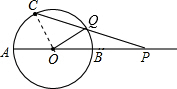
解：①当P在直线AB延长线上时，如图所示：
连接OC，
设=x°，
∵PQ=OQ，
∴∠OQP=∠CPO=x°，
∴∠CQO=2x°，
∵OQ=OC，
∴∠OCQ=∠CQO=2x°，
∵点C为半圆上的三等分点，
∴∠AOC=60°，
∴x+2x=60，
∴x=20°，
∴∠CPO=20°，
②当P在直线BA延长线上时，∠CPO=40°；
③当P在线段AB上时，∠CPOO=100°，
故答案为：20°或40°或100°
解：①当P在直线AB延长线上时，如图所示：连接OC，
设=x°，
∵PQ=OQ，
∴∠OQP=∠CPO=x°，
∴∠CQO=2x°，
∵OQ=OC，
∴∠OCQ=∠CQO=2x°，
∵点C为半圆上的三等分点，
∴∠AOC=60°，
∴x+2x=60，
∴x=20°，
∴∠CPO=20°，
②当P在直线BA延长线上时，∠CPO=40°；
③当P在线段AB上时，∠CPOO=100°，
故答案为：20°或40°或100°
点评：本题考查了圆心角和所对弧之间的数量关系和三角形的外角和定理，根据n°的圆心角对着n°的弧以及一条弧所对的圆周角等于它所对的圆心角的一半，得圆周角的度数等于它所对的弧的度数的一半即可解决问题．
练习册系列答案
相关题目
22、如图，已知AB为⊙O的直径，C为⊙O上一点，CD⊥AB于D，AD=9，BD=4，以C为圆心，CD为半径的圆与⊙O相交于P，Q两点，弦PQ交CD于E，则PE•EQ的值是（ ）
如图，已知AB为半⊙O的直径，直线MN与⊙O相切于C点，AE⊥MN于E，BF⊥MN于F．
如图，已知AB为⊙O的直径，直线l与⊙O相切于点D，AC⊥l于C，AC交⊙O于点E，DF⊥AB于F．
（2012•包头）如图，已知AB为⊙O的直径，过⊙O上的点C的切线交AB的延长线于点E，AD⊥EC于点D且交⊙O于点F，连接BC，CF，AC．
（2012•呼和浩特）如图，已知AB为⊙O的直径，PA与⊙O相切于点A，线段OP与弦AC垂直并相交于点D，OP与弧AC相交于点E，连接BC．