题目内容
（2012•柳州二模）若一弧长为π的弧所对的圆心角为60°，那么它所对的弦长为
3
3
．分析：根据弧长公式l=
求出R的大小，由弧所对的圆心角为60°可得出两半径与弧所对的弦构成等边三角形，继而可得出弦的长．
| nπ×R |
| 180 |
解答：解：由题意得，l=π=
，
则可得R=3，
又∵弧所对的圆心角为60°，
∴两半径与弧所对的弦构成等边三角形，
故可得所对的弦长=R=3．
故答案为：3．
| 60π×R |
| 180 |
则可得R=3，
又∵弧所对的圆心角为60°，
∴两半径与弧所对的弦构成等边三角形，
故可得所对的弦长=R=3．
故答案为：3．
点评：本题考查了弧长的计算及等边三角形的判定及性质，根据弧长公式求出半径R是解答本题的关键，难度一般，要求我们熟练掌握一些基础知识．
练习册系列答案
相关题目
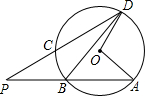（2012•柳州二模）如图，在⊙O中，弦AB、DC的延长线相交于点P．如果∠AOD=110°，∠BDC=20°，那么∠P=（ ）