Question

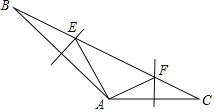
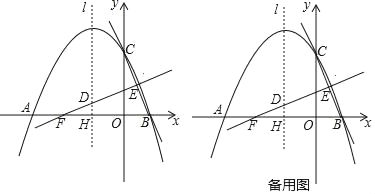
【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，4），线段BC的中垂线与对称轴l交于点D，与x轴交于点F，与BC交于点E，对称轴l与x轴交于点H．

（1）求抛物线的函数表达式；

（2）求点D的坐标；

（3）点P为x轴上一点，⊙P与直线BC相切于点Q，与直线DE相切于点R．求点P的坐标；

（4）点M为x轴上方抛物线上的点，在对称轴l上是否存在一点N，使得以点D，P，M．N为顶点的四边形是平行四边形？若存在，则直接写出N点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线表达式为：y=﹣（x+4）（x﹣2）=﹣x2﹣x+4；（2）点D坐标为（﹣1，1）；（3）点P坐标为（，0）或（7，0）；（4）存在（﹣1，）、（﹣1，）、（﹣1，﹣）

【解析】（1）利用待定系数法问题可解；

（2）依据垂直平分线性质，利用勾股定理构造方程；

（3）由题意画示意图可以发现由两种可能性，确定方案后利用锐角三角函数定义构造方程，求出半径及点P坐标；

（4）通过分类讨论画出可能图形，注意利用平行四边形的性质，同一对角线上的两个端点到另一对角线距离相等．

（1）∵抛物线过点A（﹣4，0），B（2，0）

∴设抛物线表达式为：y=a（x+4）（x﹣2）

把C（0，4）带入得

4=a（0+4）（0﹣2）

∴a=﹣，

∴抛物线表达式为：y=﹣（x+4）（x﹣2）=﹣x2﹣x+4

（2）由（1）抛物线对称轴为直线x=﹣=﹣1，

∵线段BC的中垂线与对称轴l交于点D，

∴点D在对称轴上，

设点D坐标为（﹣1，m），

过点C做CG⊥l于G，连DC，DB，

∴DC=DB，

在Rt△DCG和Rt△DBH中

∵DC2=12+（4﹣m）2，DB2=m2+（2+1）2

∴12+（4﹣m）2=m2+（2+1）2

解得：m=1

∴点D坐标为（﹣1，1）；

（3）∵点B坐标为（2，0），C点坐标为（0，4）

∴BC=，

∵EF为BC中垂线

∴BE=

在Rt△BEF和Rt△BOC中，

cos∠CBF=,

∴,

∴BF=5，EF=，OF=3

设⊙P的半径为r，⊙P与直线BC和EF都相切，

如图：

①当圆心P1在直线BC左侧时，连P1Q1，P1R1，则P1Q1=P1R1=r1

∴∠P1Q1E=∠P1R1E=∠R1EQ1=90°

∴四边形P1Q1ER1是正方形

∴ER1=P1Q1=r1

在Rt△BEF和Rt△FR1P1中

tan∠1=，

∴，

∴r1=，

∵sin∠1=，

∴FP1=，OP1=，

∴点P1坐标为（，0）

②同理，当圆心P2在直线BC右侧时，

可求r2=，OP2=7

∴P2坐标为（7，0）

∴点P坐标为（，0）或（7，0）

（4）存在，

当点P坐标为（，0）时，

①若DN和MP为平行四边形对边，则有DN=MP

当x=时，y=﹣，

∴DN=MP=

∴点N坐标为（﹣1，）

②若MN、DP为平行四边形对边时，M、P点到ND距离相等

则点M横坐标为﹣

则M纵坐标为﹣，

由平行四边形中心对称性可知，点M到N的垂直距离等于点P到点D的垂直距离，

当点N在D点上方时，点N纵坐标为，

此时点N坐标为（﹣1，），

当点N在x轴下方时，点N坐标为（﹣1，﹣），

当点P坐标为（7，0）时，所求N点不存在．

故答案为：（﹣1，）、（﹣1，）、（﹣1，﹣）