题目内容
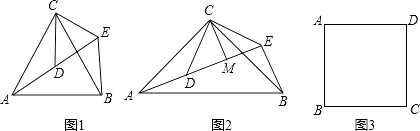
【题目】如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.

(1)当AB=2时,求GC的长;
(2)求证:AE=EF.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
试题(1)由△ABE∽△ECG,得到AB:EC=BE:GC,从而求得GC的长即可求得S△GEC;
(2)取AB的中点H,连接EH,利用ASA证明△AHE≌△ECF,从而得到AE=EF;
试题解析:(1)∵AB=BC=2,点E为BC的中点,∴BE=EC=1,∵AE⊥EF,∴△ABE∽△ECG,∴AB:EC=BE:GC,即:2:1=1:GC,解得:GC=![]() ,∴S△GEC=
,∴S△GEC=![]() ECCG=
ECCG=![]() ×1×
×1×![]() =
=![]() ;
;
(2)取AB的中点H,连接EH,∵ABCD是正方形,AE⊥EF,∴∠1+∠AEB=90°,∠2+∠AEB=90°,∴∠1=∠2,∵BH=BE,∠BHE=45°,且∠FCG=45°,∴∠AHE=∠ECF=135°,AH=CE,∴△AHE≌△ECF,∴AE=EF;

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目