题目内容
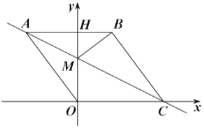
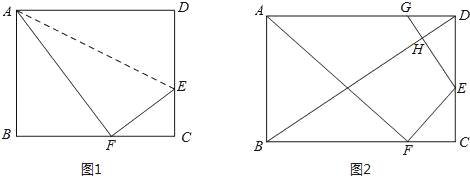
【题目】如图，
中，
，
，
，点
是
的中点，将
沿
翻折得到
，连
，则线段的长等于（ ）
A.
B.
C.
D.
【答案】D
【解析】
如图连接BE交AD于O，作AH⊥BC于H．首先证明AD垂直平分线段BE，△BCE是直角三角形，求出BC、BE，在Rt△BCE中，利用勾股定理即可解决问题．
解：如图连接BE交AD于O，作AH⊥BC于H．
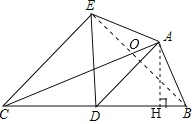
在Rt△ABC中，∵AC=12，AB=5，
∴BC=
，
∵CD=DB， ∴AD=DC=DB=6.5，
∵
BCAH=ABAC，
∴AH=
，
∵AE=AB， ∴点A在BE的垂直平分线上．
∵DE=DB=DC， ∴点D在BE的垂直平分线上，△BCE是直角三角形，
∴AD垂直平分线段BE，
∵ ADBO=BDAH， ∴OB=，
∴BE=2OB= 
，
在Rt△BCE中，EC= 
故选：D．
练习册系列答案
相关题目
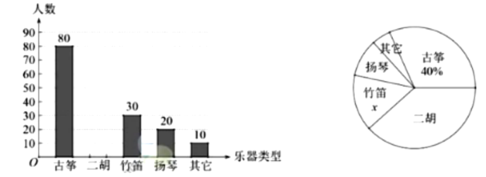
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了部分学生的得分进行统计：
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
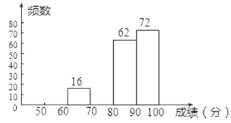
请你根据以上的信息，回答下列问题：
（1）
，
；
（2）在扇形统计图中，“成绩
满足
”对应扇形的圆心角的度数是 ；
（3）若将得分转化为等级，规定：评为
，
评为
，
评为
，
评为
．这次全校参加竞赛的学生约有 人参赛成绩被评为“”．
