题目内容
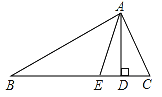
【题目】已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C﹣∠B有怎样的数量关系?说明理由.
【答案】(1)10°;(2)∠DAE=![]() (∠C-∠B).
(∠C-∠B).
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°﹣∠B﹣∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C﹣∠B的关系.
试题解析:解:∵∠ABC=30°,∠ACB=50°,∴∠CAB=180°﹣∠B﹣∠C=100°,∵AE是△ABC角平分线,∴∠CAE=![]() ∠CAB=50°,∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90°﹣∠C=40°,∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
∠CAB=50°,∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90°﹣∠C=40°,∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
(2)∠DAE=![]() (∠ACB﹣∠ABC),理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=
(∠ACB﹣∠ABC),理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=![]() (180°﹣∠B﹣∠C),∴∠DAE=
(180°﹣∠B﹣∠C),∴∠DAE=![]() (180°﹣∠B﹣∠C)﹣(90°﹣∠C)=
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B).
(∠C﹣∠B).

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目




